Ombre31 a écrit:Désolé d'avoir mis 2 jours à répondre, je n'avais pas Internet ce week-end ! Dans mon cas, A est positif et B est négatif (j'aurai dû préciser c'est vrai...).
Je vais essayer de creuser ta piste Yezu, je n'y avais pas pensé !
Après, vu la primitive donnée par Wolfram, je sais pas si j'ai envie de continuer à le faire à la main... x)
C'est un peu naïf de dire cela:
En effet, j'ai tout de même demandé le signe des constantes car le calcul en dépend. Ensuite Wolfram ce n'est qu'une machine qui en particulier ne se pose pas la question du signe des constantes!!!!
Les différents intervenants t'ont donné la démarche donc pas besoin de Wolfram.
Je résume l'aide et j'avance un peu les choses
tu est amené à calculer
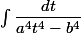
( maintenant a,b sont>0)
En effectuant le changement de variable x=a/bt, l'intégrale se ramène au calcul de à
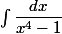
Et il bien connu que pour intégrer une fraction rationnelle il faut la mettre sous sa forme simple,i.e .
(x+1)(x^2+1)}=\dfrac{1}{4 (-1+x)}-\dfrac{1}{4 (1+x)}-\dfrac{1}{2 \left(1+x^2\right)})
reste à calculer la primitive de chaque terme ce qui se fait facilement.
Maintenant concernant l'idée de @Yezu, c'est bien d'avoir des idées mais il faut parfois se dire si cela vaut le coup de poursuivre. A mon avis non, en effet il résout avec B=0. Mais ici l'équation n'est pas linéaire donc il vaut mieux rester avec la résolution préconisée ci-dessus.
Modifié en dernier par aviateur le 25 Juin 2018, 10:25, modifié 1 fois.
