Problème de Maths Stats Loi Poisson

[ObiwanK78]

On a X1,X2,...,X50 qui suivent indépendamment une loi P(1)
Y=Somme(1 à 50) des Xi~P(50)

1. Calculer P(Y>2)
2. Donner une approximation du résultat avec le théorème de la limite centrale

URGENT SVP

[LB2]

Bonjour,

un peu de politesse serait appréciable. Essaie de dire bonjour avant de donner un énoncé, et les "URGENT SVP" sont proscrits.
Ensuite, qu'as-tu cherché? Le forum n'est pas un site de corrigés...

Déjà, peux-tu donner l'expression de la fonction de répartition des Xi ? Donc la fonction de répartition de Y = ? En particulier peux-tu justifier que Y suit une loi de poisson P(50) ?

Quel est le lien entre la fonction de répartition de Y et P(Y>2) ?

2 . Qu'est-ce que le théorème de la limite centrale? Autrement dit, la loi de Y se rapproche de quelle loi usuelle?

Cordialement

[ObiwanK78]

Excuse moi je suis nouveau à vrai dire je fais des maths en anglais j'ai peut être mal traduit l'énoncé je suis vraiment bloque et c'est important pour mes partiels en fait.. je ne sais pas comment ajouter une image ? Ou si tu veux je te donne mon adresse mail pour te l'envoyer ? J'en ai vraiment besoin ^^

Merci d'avance !

[LB2]

Il n'y a pas d'erreur d'énoncé a priori, si tu l'as bien recopié ici. Je t'ai donné des indications, à toi de travailler maintenant.

Cordialement

[ObiwanK78]

En fait on a {\sqrt{}}{n}\times \frac{Xn - \mu}{\sigma}\rightarrow N(0;1)

[ObiwanK78]

Ah et Xn=X1+X2+...+Xn/n

[ObiwanK78]

Et sinon je dirais que Y se rapproche d'une loi binomiale non ?
Ou normale avec ce qui précède mais je ne vois pas comment exprimer P(Y>2)

[LB2]

OK pour l'expression du théorème central limite : il s'agit d'une convergence en loi. En pratique, pour n grand, on peut approximer la loi de 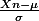par une loi normale centrée réduite.
Il faut connaitre la conséquence de ce TCL dans le cas particulier d'une somme de lois de Poisson indépendantes. La règle pratique pour une loi de Poisson de paramètre est que si 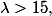on peut l'approximer par une loi normale de même moyenne.

Autrement dit, pour calculer ce qui t'intéresse , tu as deux possibilités :

- un calcul exact où tu utilise la formule de la loi de Poisson P(50).
- un calcul approché où Z suit une loi normale

Comme on ne dispose que de la table des valeurs des quantiles de la loi normale centrée réduite , il faut écrire qui est très proche de 1.

Es tu sur que c'est bien p(Y>2) que tu veux calculer, et pas p(Y>20) par exemple? Cela paraitrait plus raisonnable...

[ObiwanK78]

Okay je vais mettre ça au propre et je te redis Merci beaucoup !
Simplement je ne savais pas pour l'approximation Poisson Normale c'est une définition ou bien ?

[LB2]

En fait on a les approximations suivantes :

- La loi binomiale B(n,p) est approximée à par une loi de Poisson de paramètre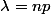 quand n est "grand" et p "petit"
- La loi binomiale B(n,p) est approximée par une loi normale de moyenne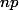 et de variance si n est "grand" et p pas trop proche de 0 ou de 1.
- La loi de Poisson de paramètre est approximée par une loi normale de moyenne et de variance si est "grand"

http://www.bibmath.net/formulaire/index ... pproximloi

[ObiwanK78]

Super merci je vais écrire ça au propre, comment on insère une image ou si tu veux je te laisse mon mail ? Pour être sûr de la rigueur car c'est un devoir qui est vraiment important ^^

[LB2]

Pas de mail mais tu peux insérer une image sur le forum par exemple avec https://www.noelshack.com/ en partageant le lien

[ObiwanK78]

[ObiwanK78]

La 1. Mais c'est presque 1 la probabilite c'est vraiment bizarre, la je vais faire l'approximation

[LB2]

Oui c'est bizarre, la proba p(Y>2) vaut environ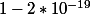
Je me demande s'il y a une erreur d'énoncé...

Dans ce que tu as écrit, attention on n’utilise pas l'approximation normale dans la question 1. C'est seulement dans la question 2. Dans la question 1, on utilise juste la définition de la loi de Poisson

[ObiwanK78]

Est ce juste ?

Effectivement la proba est très proche de 1 alors soit le prof nous troll soit je sais pas...