Question trigonométrie pour jeu vidéo

[jurams]

Bonjour à tous,

Je développe un jeu 2D en C++, qui dit 2D dit géométrie
Vu mon niveau j'ai assez de mal à avancer, j'ai donc une question :

Ma question est assez simple et je pense que vous allez rigoler en lisant celle-ci :

J’aimerai obtenir la position (x et y) du point B sur le cercle seulement en connaissant le rayon ainsi que l'angle.

L'image :


Merci beaucoup d'avance.

Cordialement.

[Lostounet]

Salut,
Si on trace la droite horizontale qui va vers la droite (tu as tracé la verticale il me semble), on trouve que l'angle entre l'horizontale et le rayon r (que tu as tracé) est de 5 degrés.

Ce qui signifie que le point B a pour coordonnées (15cos(5°); 15 sin(5°)).

Bien entendu... cela suppose que le repère choisi est le repère "classique" (le cercle a pour centre (0,0), que les axes sont "comme il faut" etc..)

[jurams]

Salut Lostounet,

Merci beaucoup pour ta réponse,
effectivement cette méthode fonctionne de 0 à 90° mais si je me trompe pas pour
les angles au dessus de 90° la fonction doit surement être changé et là je suis perdu...

Veuillez excusez mon manque de connaissance basique,
D'ailleurs si vous connaissez un bon livre de mathématique pédagogique revoyant les bases
en géométrie je suis preneur

Merci

[Lostounet]

Salut Lostounet,

Merci beaucoup pour ta réponse,
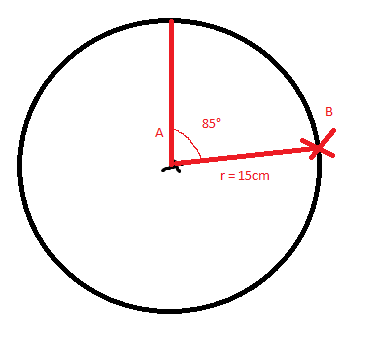
effectivement cette méthode fonctionne de 0 à 90° mais si je me trompe pas pour
les angles au dessus de 90° la fonction doit surement être changé et là je suis perdu...

Veuillez excusez mon manque de connaissance basique,
D'ailleurs si vous connaissez un bon livre de mathématique pédagogique revoyant les bases
en géométrie je suis preneur

Merci

Je crois que je comprends ta question !
Si tu choisis un autre angle, admettons 100 degrés sur ton dessin, cela signifierait que tu as un angle entre B et l'horizontale qui est de 10 degrés, mais vers le bas (90 - 100 = -10)! Donc B ferait un angle de -10 degrés avec l'horizontale (on marche dans le sens horaire).
B aurait donc comme coordonnées (15cos(-10° ); 15 sin(-10° ) )

Une autre vision des choses, si tu n'aimes pas les nombres négatifs: tu tournes dans l'autre sens, et tu te dis que l'angle entre l'horizontale et B, parcouru dans le sens antihoraire, serait de 360° - 10° = 350°. (si tu fais un dessin, ce sera simple à voir).

B aurait donc comme coordonnées (15cos(350°); 15 sin(350° ) ) ... et les réponses sont les mêmes puisque cos(-10°) = cos(350°)
et sin(-10°) = sin(350°)

Donc de toute manière, la règle est de calculer l'angle (un angle...) que fait B avec l'horizontale (dans le sens que tu veux). Vu que tu as l'angle entre B et A, une simple soustraction suffit.

[jurams]

D'accord j'ai tout compris !
Merci à toi Lostounet.

Il faut que je fasse juste une équation pour avoir l'angle entre B et l'horizontale en fonction de l'angle
sur le dessin et ce sera parfait.

[Lostounet]

Oui... as-tu donc une idêe de la formule générale (qui se dégage d'après les exemples) des coordonnées lorsqu'on prend un angle quelconque x ?

On fait 90-x... puis B a pour coordonnées ....

[jurams]

je t'avoue que je ne vois pas de quelle formule il s'agit même si je suis sur de l'avoir vu en cour.
Ça me dit quelque chose.

[Lostounet]

je t'avoue que je ne vois pas de quelle formule il s'agit même si je suis sur de l'avoir vu en cour.
Ça me dit quelque chose.

Tu n'as pas besoin du cours ! Il suffit de réecrire la formule que je t'ai proposée avec des exemples !
On a pris l'exemple x = 85 et x = 100

Puis on a déduit que B(15cos(90 - 85), 15*sin(90 - 85))

Il suffit de remplacer 85 par x pour obtenir une formule générale et essayer de l'implémenter...!

[jurams]

Ah oui je pensais que tu me demandais le nom de l'équation, je t'avais mal compris.
Effectivement, dans B(√(15)* cos(90 - 85), √(150*sin(90 - 85)) je remplace 15 par le rayon et 85 par notre angle.

[Lostounet]

Oui...

Ce chapitre s'appelle "cercle trigonométrique" si jamais tu en as besoin !

[Ben314]

Salut,
@Lostounet : tu peut m'expliquer d'où il sort ton racine(15) que tu traîne depuis le début ?

Sinon, si c'est pour un truc d'info, faire gaffe aussi qu'assez souvent, l'axe des y est dirigé vers le bas (et le point (0,0) est en haut à gauche de la fenêtre)

[Lostounet]

Salut,
@Lostounet : tu peut m'expliquer d'où il sort ton racine(15) que tu traîne depuis le début ?)

Mince...
Mon manque de sommeil a fini par me rattraper ! En plus j'ai mis ça à tous les messages

Vraiment désolé ! Je rectifie...

Les coordonnées (polaires) de B sont de la forme (rcos(x) ; rsin(x)). Il n'y a aucune racine carrée...