Bonjour,
Je suis bloqué sur un exercice dans lequel je dois prouver que l’anneau quotient C[x, y]/<(x+1)(y−1)i> est isomorphe au sous-anneau de C[x] × C[y] des paires de polynômes (P(x), Q(y)) tel que P(−1) = Q(1).
J'ai d'abord pensé utiliser le premier théorème d'isomorphisme en prenant phi : C[x,y] -> {sous-anneau de C[x] x C[y]}, et en calculant son noyau. Mais je n'arrive pas à définir l'homomorphisme phi. Est- ce que vous avez des idées ?
Merci d'avance !
Isomorphisme d'anneaux
6 messages
- Page 1 sur 1
Re: Isomorphisme d'anneaux
Bonjour
La famille^m(y-1)^n) pour
pour \in\N^2) est une base de
est une base de 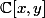 . Ecris un polynôme
. Ecris un polynôme  sur cette base, et regarde...
sur cette base, et regarde...
PS: Dans C[x, y]/<(x+1)(y−1)i> il y a bien un i?
La famille
PS: Dans C[x, y]/<(x+1)(y−1)i> il y a bien un i?
Re: Isomorphisme d'anneaux
Salut,
Sinon, concernant ta question, si tu veut construire un morphisme de dans
dans 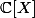 , ce qui devrait te venir à l'esprit, c'est les applications de la forme
, ce qui devrait te venir à l'esprit, c'est les applications de la forme \mapsto P(X,\beta)) avec
avec  fixé.
fixé.
De même pour les morphisme de dans
dans  : ceux de la forme
: ceux de la forme \mapsto \Big(\!P(X,\beta)\,,\,P(\alpha,Y)\Big))) (avec
(avec  fixés) semblent on ne peut plus naturels.
fixés) semblent on ne peut plus naturels.
Et si tu prend un soupçons de recul, en fait, ces trucs, ce sont les morphismes classiques "d'évaluation" :\mapsto P(\lambda)) pour
pour  fixé où tu as regardé
fixé où tu as regardé  comme du
comme du  avec
avec  (ou bien comme du
(ou bien comme du 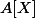 avec
avec  ).
).
Sinon, concernant ta question, si tu veut construire un morphisme de
De même pour les morphisme de
Et si tu prend un soupçons de recul, en fait, ces trucs, ce sont les morphismes classiques "d'évaluation" :
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Isomorphisme d'anneaux
Salut,
D'abord oui effectivement il ne devrait pas y avoir de i !
Merci beaucoup pour vos réponses je crois que j'ai finalement réussi à résoudre cet exercice :
si on prend le morphisme d'évaluation -> (f(x,1), f(-1,y))) on a bien P(-1) = Q(1), et il n'y a plus qu'à prouver que son noyau est
on a bien P(-1) = Q(1), et il n'y a plus qu'à prouver que son noyau est (y-1)>) c'est bien ça ?
c'est bien ça ? 
D'abord oui effectivement il ne devrait pas y avoir de i !
Merci beaucoup pour vos réponses je crois que j'ai finalement réussi à résoudre cet exercice :
si on prend le morphisme d'évaluation
Re: Isomorphisme d'anneaux
Oui (et non...)
Il faut effectivement prouver que :
(i) Le noyau c'est l'idéal engendré par (X+1)(Y-1).
(ii) L'image est contenue dans l'ensemble des couples (P,Q) tels que P(-1)=Q(1)
Mais aussi que :
(iii) Tout les couples (P,Q) tels que P(-1)=Q(1) sont atteints par la fonction (pour avoir la surjectivité de la fonction qui est bien évidement nécessaire à la bijectivité).
Il faut effectivement prouver que :
(i) Le noyau c'est l'idéal engendré par (X+1)(Y-1).
(ii) L'image est contenue dans l'ensemble des couples (P,Q) tels que P(-1)=Q(1)
Mais aussi que :
(iii) Tout les couples (P,Q) tels que P(-1)=Q(1) sont atteints par la fonction (pour avoir la surjectivité de la fonction qui est bien évidement nécessaire à la bijectivité).
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 50 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
