Groupe de matrice

[zzzzaaa]

Bonjour,

Voici l'exo (problème) https://image.noelshack.com/fichiers/20 ... img026.jpg

Pour la 2)c) je vois pas trop comment utiliser Im fA. Je vois bien que je peux faire un changement de base en prenant comme nouvelle base de R^n une base de ker fA concaténé à une base de son complémentaire, mais j'ai rien qui me dit que c'est Im fA ?

Pour la 3)a), je vérifie comment ? Je recopie bêtement les matrices avec des coefficients arbitraires et je fais le truc à la main ? C'est long et pas très intéréssant

Je suis toujours bloqué sur la 4e propriété de 4)a) qui ressemble en fait a ce qui a été fait en 2)c)

Merci

[pascal16]

2c) https://fr.wikipedia.org/wiki/Th%C3%A9o ... me_du_rang

3a) pourquoi ne pas écrire que le coefficient ij = somme ....
on fait quelques sous-cas pour les colonnes et lignes de zéros.
ensuite on tronque la somme pour la partie supérieur gauche 'XY' et on retombe sur le produit de matrice XY

4a) on ne passa pas plutôt pas le fait qu'on est dans un groupe, donc on a des inverses ?

[Ben314]

Salut,
Déjà, concernant le 2)c), ça serait pas con... d'apprendre à lire un énoncé... : là, on te dit de trouver une matrice P telle que pour tout A, etc..., ce qui signifie que la matrice P, ben c'est la même pour toutes les matrices A et donc que c'est sûrement pas du coté de im(f_A) qu'il faut regarder vu qu'à priori, il dépend de A.
Par contre, la "matrice neutre" E, elle, elle dépend de rien du tout et c'est elle qui va te donner P.
Et c'est relativement couillon vu la question précédente où on t'a fait constater que E est une projection, donc il suffit de prendre pour P une des matrices de changement de base qui envoie les r première coordonnées de la base canonique sur une base de im(f_E) et les autres sur une base de ker(f_E) pour que ton truc soit vérifié.

[zzzzaaa]

Pourquoi est il dit qu'ilfaut utiliser im fa et ker fA si c'est la matrice E qu'il faut utiliser alors ?

[Ben314]

Un truc de ce style écrit entre parenthèse, ça s’appelle une indication, et si y'a un truc de sûr et certain, c'est que c'est pas une indication qui va changer l'énoncé de la question qui, ici, te demande on ne peut plus clairement de déterminer une matrice P indépendante de A telle que...

Et cette indication, ici, elle t'indique que tu devrait chercher quel lien il y a entre im(f_A) et ker(f_A) d'un coté (qui dépendent à priori de A) et im(f_E) et ker(f_E) de l'autre (qui eux ne dépendent de rien du tout) qui sont on ne peu plus clairement les "bons" candidats pour fabriquer une nouvelle base (et donc une matrice de passage P).

[Pseuda]

Bonsoir,

Indication pour la 2)c) : tu peux prendre, comme dit Ben314 dans son langage fleuri , une matrice P de passage de la base canonique à une base constituée d'une base de Im(f_E) et d'une base de Ker(f_E).

Pour que la matrice de f_A s'écrive ainsi dans la nouvelle base, il faut montrer que :

1) si x appartient à Im(f_E), alors f_A(x) appartient aussi à Im(f_E) (autrement dit, Im(f_E) stable par f_A)) : utilise que f_E est élément neutre pour f_A : f_A o f_E= f_A o f_E = f_A

2) si x appartient à Ker(f_E), alors f_A(x)=0 (idem).

[Pseuda]

Pour la 3)a), je vérifie comment ? Je recopie bêtement les matrices avec des coefficients arbitraires et je fais le truc à la main ? C'est long et pas très intéréssant

Je suis toujours bloqué sur la 4e propriété de 4)a) qui ressemble en fait a ce qui a été fait en 2)c)

Bonsoir,

Pour la 3)a), c'est une ligne : on utilise le produit de matrices par blocs (même calcul que le produit de matrices).

Pour la 4)a), il suffit de montrer que (en utilisant le théorème du rang et la formule de Grassmann). On prend un vecteur à l'intersection de ces 2 sous-espaces vectoriels ...

[zzzzaaa]

Bonsoir,

Indication pour la 2)c) : tu peux prendre, comme dit Ben314 dans son langage fleuri , une matrice P de passage de la base canonique à une base constituée d'une base de Im(f_E) et d'une base de Ker(f_E).

Pour que la matrice de f_A s'écrive ainsi dans la nouvelle base, il faut montrer que :

1) si x appartient à Im(f_E), alors f_A(x) appartient aussi à Im(f_E) (autrement dit, Im(f_E) stable par f_A)) : utilise que f_E est élément neutre pour f_A : f_A o f_E= f_A o f_E = f_A

2) si x appartient à Ker(f_E), alors f_A(x)=0 (idem).

Merci c'est plus clair, du coup en faisant le changement de base : M(fA) relativement à la base canonique de R^n vers M(fA) relativement à la base de R^n obtenu en concaténant les bases de Ker fE et Im fE, on obtient P qui vaut la matrice de passage de la base canonique vers la base de ker fe+im fe

et on trouve que la nouvelle matrice obtenue "au milieu" est bien de la forme voulue car elle vaut 0 quasi-partout avec un bloc en haut à gauche qui vaut la matrice M de fA restreinte à Im fE relativement à la base de Im fE ?

Pour la 3)a), je vérifie comment ? Je recopie bêtement les matrices avec des coefficients arbitraires et je fais le truc à la main ? C'est long et pas très intéréssant

Je suis toujours bloqué sur la 4e propriété de 4)a) qui ressemble en fait a ce qui a été fait en 2)c)

Bonsoir,

Pour la 3)a), c'est une ligne : on utilise le produit de matrices par blocs (même calcul que le produit de matrices).

Pour la 4)a), il suffit de montrer que (en utilisant le théorème du rang et la formule de Grassmann). On prend un vecteur à l'intersection de ces 2 sous-espaces vectoriels ...

Je n'ai pas vu le calcul par bloc... Je me suis débrouillé en raisonnant sur un coefficient (plus simple) en fonction de i (ligne) et j (colonne) puis après j'ai scindé les cas particuliers selon si i et j sont tous les deux dans [[1,r]] ou non

Et oui suis-je bête, j'avais oublié cette propriété...
Si on prend v dans l'intersection, alors f(v) = 0 et v=f(u) avec u vecteur quelconque de R^n, donc f^2(u) = 0 or Ker f = Ker f^2 donc u€Ker f donc f(u)=0 donc v = 0
Donc l'intersection est nulle On a donc bien le fait qu'ils sont supplémentaires.

---

En revanche je viens de me rendre compte pour la 4)b), P et M peuvent dépendre de A ? Autant refaire la même chose qu'avant... Ou alors j'ai mal compris quelque chose car cela voudrait dire que toutes les matrices sont égales...

Pour la fin, le groupe M^k à l'air d'être assez évidemment un sous-groupe vu que M^q * M^p = M^(p+q) (stable), c'est non vide et on peut trouver un symétrique de M^k avec M^(-k)
Du coup A appartient au groupe G définit à la question 3 ? Mais du coup je vois pas trop l'utilité de ce que je viens de démontrer juste avant

Et encore merci ^^

[Pseuda]

Merci c'est plus clair, du coup en faisant le changement de base : M(fA) relativement à la base canonique de R^n vers M(fA) relativement à la base de R^n obtenu en concaténant les bases de Ker fE et Im fE, on obtient P qui vaut la matrice de passage de la base canonique vers la base de ker fe+im fe

et on trouve que la nouvelle matrice obtenue "au milieu" est bien de la forme voulue car elle vaut 0 quasi-partout avec un bloc en haut à gauche qui vaut la matrice M de fA restreinte à Im fE relativement à la base de Im fE ?

On a d'abord P et on obtient M(fA)=A par rapport aux bases Im(fE)+Ker(fE). Il faut montrer que la matrice obtenue a la forme voulue : expliquer pourquoi elle vaut 0 pour les colonnes de droite (celles correspondant à Ker(fE), et pourquoi elle vaut M_A d'ordre r et inversible pour les colonnes de gauche.

L'indication est fausse. Il faut utiliser Im(fE) et Ker(fE).

[zzzzaaa]

P c'est la matrice de passage donc dès qu'on fait le changement de base, P et P^-1 apparaissent

Ensuite pour tous les vecteurs de la base de ker fE, comme ils sont aussi dans ker fA alors ça fait que des colonnes de 0 pour ces vecteurs là
Et pour les vecteurs de la base de Im fE, comme on reste dans Im fE en appliquant f, on obtient une matrice carrée d'ordre r.

[Pseuda]

En revanche je viens de me rendre compte pour la 4)b), P et M peuvent dépendre de A ? Autant refaire la même chose qu'avant... Ou alors j'ai mal compris quelque chose car cela voudrait dire que toutes les matrices sont égales...

Pour la fin, le groupe M^k à l'air d'être assez évidemment un sous-groupe vu que M^q * M^p = M^(p+q) (stable), c'est non vide et on peut trouver un symétrique de M^k avec M^(-k)
Du coup A appartient au groupe G définit à la question 3 ? Mais du coup je vois pas trop l'utilité de ce que je viens de démontrer juste avant

Et encore merci ^^

Bonjour,

Pour la 4)c), A est quelconque de rang r : on n'est pas dans les mêmes conditions que 2)c) où A appartenait à un groupe de matrices. Dans une base adaptée à f_A, la matrice de f_A a la forme voulue (c'est presque du cours).

Puis, A restant toujours quelconque de rang r (donc rien à voir avec les questions 2 et 3), il faut définir un groupe de matrices contenant A (ce groupe paraît assez évident, donc faire une conjecture et la démontrer).

[zzzzaaa]

Je ne sais pas ce qu'est une « base adaptée » ?

[Pseuda]

Je ne sais pas ce qu'est une « base adaptée » ?

Base de l'espace vectoriel E adaptée à un sous-espace vectoriel F : base de E dont une sous-famille est une base de F.
https://www.panamaths.net/Documents/Syn ... TABLES.pdf


Ici puisque Im(f_A) et Ker(f_A) sont supplémentaires (remarque : ce n'est pas toujours le cas pour un endomorphisme), une base de E adaptée à la supplémentarité de ces sous-espaces vectoriels (ou adaptée à f_A, mais ceci est peut-être un abus de ma part), c'est une base de E construite en juxtaposant une base de Im(f_A) et une base de Ker(f_A). Dans cette base, la matrice de f_A a la forme de la matrice par blocs du 4).

[Pseuda]

Bonjour,

Remarque : dans tout ça, f_E est une projection (car f_E o f_E = f_E), mais pas forcément f_A, qui peut être par exemple la composée d'une projection sur Im(f_E) et d'une rotation (ou de toute autre application linéaire) dans Im(f_E). (ce me semble, mais pas le temps d'aller plus loin).

[zzzzaaa]

Pourtant la matrice de la 3) est exactement la même que la 4 :

P et P-1 sont dans GLn(R) dans les deux cas, M est dans un sous groupe de Gl_r dans les deux cas ?

[Pseuda]

Bonsoir,

M appartient à un sous-groupe de dans les 2 cas. Et alors ? Je ne comprends pas bien le but de ta question. On n'est pas dans le même contexte en fonction des questions :

1) on donne un exemple de groupe de matrices
2) on montre que si est un groupe de matrices, ses matrices sont semblables dans une certaine base (celle du 2)) à des matrices qui s'écrivent par blocs de la même façon en fonction du rang de , la matrice de l'élément neutre
3) on donne un 2ème exemple de groupe de matrices, qui constitue en fait la réciproque du 2), et donc la forme la plus générale d'un groupe de matrices
4) on part d'une matrice quelconque, et on montre qu'il existe au moins un groupe de matrices qui la contient ssi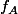 vérifie la condition du b). Cette question est déconnectée dans ses hypothèses des questions 2) et 3).

On part d'un groupe de matrices, d'élément neutre . Dans une certaine base (la base du 2)), la matrice de (l'application canoniquement associée à , c'est une projection) est une matrice par blocs constituée de 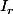( le rang de ) et des partout ailleurs. Les matrices des applications 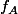sont de rang et dans cette base, s'écrivent (sont semblables à des matrices) par blocs avec de rang et des partout ailleurs.

Donc les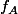 sont des composées d'une projection (sur ) et d'une application opérant dans ) (sauf erreur).