DM

[floflo61160]

Bonjour, je suis bloquée à un exercice de mon dm

Énoncé: Un menuisier propose un escalier composé de 14 marches. Ces marches présentent un défaut dans 4% des cas. Elles sont choisies indépendamment dans un stock assez important pour queces choix soient considérés comme des tirages avec remise.
Le prix de l'escalier varie suivant le nombre de défauts:
aucun ou un : 2300€ ; de deux à quatre : 1150€ ; cinq ou plus : 1000€
X est la variable aléatoire qui compte le nombre de marches ayant un défaut dans l'escalier.

Quelle est la loi de probabilité suivie de X ?
X est {0;1;2;3;4;5;6;7;8;9;10;11;12;13;14}

Calculer la probabilité, arrondie au dix-millième, que l'escalier soit vendu au prix de 2300€
n=14 ; p=4% ; k=0
p(X=0)=0.5647
n=14 ; p=4% ; k=1
p(X=1)=0.3294
Donc p(X=2300) =p(X=0)+p(X=1) =0.8941

Calculer la probabilité, arrondie au dix-millième, que l'escalier soit vendu au prix de 1150€
n=14 ; p=4% ; k=2
p(X=2) =0.0892
n=14 ; p=4% ; k=3
p(X=3) =0.0149
n=14 ; p=4% ; k=4
p(X=4) =0.0017
Donc p(X=1150)=p(X=2)+p(X=3)+p(X=4) =0.1058

Estimer le prix de vente moyen d'un escalier
Je suis coincée ici

[BenMaths]

Salut,

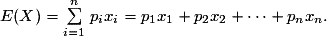
Pour commencer je ne suis pas sur que ta réponse soit suffisante pour la première question.

Quelle est la loi de probabilité suivie de X ?
X est {0;1;2;3;4;5;6;7;8;9;10;11;12;13;14}

La loi de probabilité d'une variable X ici doit faire apparaître chaque valeur possible que peut prendre X mais également en dessous la probabilité que X prenne cette valeur. Ta réponse devrait ressembler à ça :


Pour la question 2, pas de problème je n'ai pas refait le calcul mais ta démarche est bonne.
De même pour la question 3.

Pour estimer le prix de vente moyen d'un escalier il te faut plusieurs éléments. Pour l'instant tu n'as pas tout. Tu connais les prix en fonction du nombre de défaut. Tu as déjà calculé la probabilité de vendre l'escalier 2300€ (cad d'avoir 0 ou 1 défaut), la probabilité de le vendre 1150€ (la probabilité d'avoir 2,3 ou 4 défauts). Il te manque donc la dernière probabilité : celle de vendre l'escalier 1100€.

Une fois que tu auras tout ça, Il te suffit de définir une nouvelle variable aléatoire appelée Prix par exemple (qui prend comme valeur le prix auquel tu peux vendre ton escalier). Tu pourras faire sa loi de probabilité, et en calculer l'espérance. Cette espérance sera le prix moyen de vente d'un escalier.

et en cadeau la formule de l'espérance

[jordy56]

Je n'arrive pas à la question 1 pour la loi de probabilité je ne comprend pas

[jordy56]

J'ai le même exercice mais je comprend pas comment vous trouver:
n=14 ; p=4% ; k=1
p(X=1)=0.3294
Quel calcul faites vous ?