Bonsoir
J'aimerais connaître comment determiner le centre de la composée de deux rotation de centre distincte
Isometrie
8 messages
- Page 1 sur 1
Re: Isometrie
Voici mon exrecice on me donne un triangle équilatéral soit r3 et r1 des rotation s de centre respectif A et C
Que donne la transformation r3or1
Je sais que sa donne une r(#;2pi/3) mais je ne connais pas le. Centre
Que donne la transformation r3or1
Je sais que sa donne une r(#;2pi/3) mais je ne connais pas le. Centre
Re: Isometrie
Je suppose que r3 est de centre A et d'angle pi/2, et r1 est de centre C et d'angle pi/3 ?
Quel sont les images de A, B et C par r3 o r1 ?
Quel sont les images de A, B et C par r3 o r1 ?
Re: Isometrie
Salut,
Déjà, vu que tu ne connaît pas les angles des deux rotations, tu ne risque pas de savoir quel va être l'angle de la composée des deux.
Ensuite, dans un cas d'angles quelconque comme ici, on ne peut pas dire grand chose du centre de la composé (qui, bien sûr, dépend des angles des rotations) : en fait il peut être situé en n'importe quel point du plan et il est même assez intéressant de chercher à voir comment trouver les angles des deux rotations connaissant leurs centres respectifs ainsi que le centre de la rotation composée des deux.
Le outil qui marche bien pour tout ces trucs de composition de rotation, c'est de dire qu'une rotation de centre O et d'angle alpha, c'est la composée de deux réflexions d'axe deux droites passant par O et faisant un angle de alpha/2.
Bref, la réponse, c'est que le centre peut-être situé n'importe où, mais que de savoir où il est situé permet de retrouver les angles des deux rotations.
Déjà, vu que tu ne connaît pas les angles des deux rotations, tu ne risque pas de savoir quel va être l'angle de la composée des deux.
Ensuite, dans un cas d'angles quelconque comme ici, on ne peut pas dire grand chose du centre de la composé (qui, bien sûr, dépend des angles des rotations) : en fait il peut être situé en n'importe quel point du plan et il est même assez intéressant de chercher à voir comment trouver les angles des deux rotations connaissant leurs centres respectifs ainsi que le centre de la rotation composée des deux.
Le outil qui marche bien pour tout ces trucs de composition de rotation, c'est de dire qu'une rotation de centre O et d'angle alpha, c'est la composée de deux réflexions d'axe deux droites passant par O et faisant un angle de alpha/2.
Bref, la réponse, c'est que le centre peut-être situé n'importe où, mais que de savoir où il est situé permet de retrouver les angles des deux rotations.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Isometrie
Bien souvent, on commence par chercher le point fixe.
si R1 est la première rotation et R2 la seconde, on cherche un point d'affixe z tel que R2(R1(z))=z
S'il n'y en a pas, ou s'il n'y en a plusieurs, ce n'est pas une rotation.
pour simplifier les calculs
-> tu as le droit de dire que le premier centre est l'origine du repère
-> que la distance entre les deux centres de rotation est 1 (choix de l'échelle) et qu'il est en (0;1) (choix de l'orientation)
Façon géométrique :
Soit M un point M1 son image par R et M2 son image par R2oR1
Si la composée est une rotation, son centre est aussi sur la médiatrice de [MM2]
et fait pareil avec un second point
si R1 est la première rotation et R2 la seconde, on cherche un point d'affixe z tel que R2(R1(z))=z
S'il n'y en a pas, ou s'il n'y en a plusieurs, ce n'est pas une rotation.
pour simplifier les calculs
-> tu as le droit de dire que le premier centre est l'origine du repère
-> que la distance entre les deux centres de rotation est 1 (choix de l'échelle) et qu'il est en (0;1) (choix de l'orientation)
Façon géométrique :
Soit M un point M1 son image par R et M2 son image par R2oR1
Si la composée est une rotation, son centre est aussi sur la médiatrice de [MM2]
et fait pareil avec un second point
Re: Isometrie
Salut !
Tu peux passer par les nombres complexes sinon : un point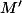 d'affixe
d'affixe  est l'image d'un point
est l'image d'un point  d'affixe
d'affixe  par la rotation de centre
par la rotation de centre  d'affixe
d'affixe  et d'angle
et d'angle  si et seulement si
si et seulement si 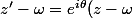) .
.
Ici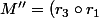(M)) équivaut à dire que
équivaut à dire que 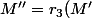) avec
avec 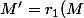) . En notant
. En notant  ,
,  et
et 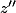 les affixes respectives des points
les affixes respectives des points  ,
, 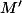 et
et 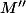 , et
, et  et
et  les affixes respectives de
les affixes respectives de  et
et  , tu obtiens deux égalités :
, tu obtiens deux égalités : 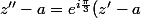) et
et 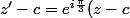) , donc finalement :
, donc finalement :
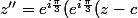+c-a) +a =...)
Je te laisse continuer
Tu peux passer par les nombres complexes sinon : un point
Ici
Je te laisse continuer
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
Re: Isometrie
Bonjour,
On sait que r3or1 est une rotation d'angle 2pi/3. On suppose que le triangle ABC est orienté de telle sorte que (en vecteurs) (AB, AC)=+pi/3 (si dans ton dessin, c'est -pi/3, il faut adapter).
r1 rotation de centre C et d'angle pi/3, envoie A en ?
r3 rotation de centre A et d'angle pi/3, envoie B en ?
donc r3or1 envoie A en ?
Le centre O de la rotation est situé sur la médiatrice de [AC], et il est tel que (en vecteurs) (OA,OC)=2pi/3. Il s'agit de trouver ce point.
Soit I le centre du triangle ABC. Que vaut (IA, IC) ? (théorème de l'angle inscrit). Donc, où est situé O ?
On sait que r3or1 est une rotation d'angle 2pi/3. On suppose que le triangle ABC est orienté de telle sorte que (en vecteurs) (AB, AC)=+pi/3 (si dans ton dessin, c'est -pi/3, il faut adapter).
r1 rotation de centre C et d'angle pi/3, envoie A en ?
r3 rotation de centre A et d'angle pi/3, envoie B en ?
donc r3or1 envoie A en ?
Le centre O de la rotation est situé sur la médiatrice de [AC], et il est tel que (en vecteurs) (OA,OC)=2pi/3. Il s'agit de trouver ce point.
Soit I le centre du triangle ABC. Que vaut (IA, IC) ? (théorème de l'angle inscrit). Donc, où est situé O ?
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 56 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
