Fonction réciproque compliquée

[LonelyGuy]

Comment calculer la fonction réciproque de ?
C'est sensé être .
PS: c'est dans le cadre d'un entraînement avec le rattrapage de l'année dernière

[mathelot]

[LonelyGuy]

OK, je viens d'arrêter de chercher, je ne sais pas si j'avais exactement trouvé mais j'en étais très proche ! Mais merci, c'est encore plus rapide comme ça de toute façon (j'avais pas pensé à faire "-y" dans votre quatrième ligne, ce qui s'avère très pratique, et c'est licite apparemment). Merci bien !

[Ben314]

Salut,
Oui, enfin c'est "licite" à condition de bien comprendre qu'en procédant de la sorte (i.e. en réutilisant deux fois la même équation) tu ne procède pas par équivalence et que tu a de forte chance d'obtenir des "solution parasites".

Par exemple, ici, si on prend la formule finale donne , sauf que si tu injecte dans la formule de départ, ça donne et tu ne retombe pas sur le de départ...

Bref, je suis pas certain du tout que ce soit super malin de procéder de la sorte (en tout cas au niveau Lycée ou il n'y a plus la moindre parcelle de logique permettant de bien comprendre qu'en procédant de la sorte on n'a pas une équivalence)

[Ben314]

Pour moi, la façon "normale" de procéder, c'est (bien évidement) par équivalence :

Sinon, normalement, pour parler de "fonction réciproque", il faut au départ clairement identifier quel est l'ensemble de départ et d'arrivé de la fonction en question, ce que tu n'a pas fait.
Mais, à condition d'admettre que l'ensemble de départ, c'est R tout entier, on peut considérer que la question c'est "Déterminer un intervalle J de R tel que g soit une bijection de R sur J et déterminer sa bijection réciproque"

Dans ce cas, à mon sens, la réponse ça doit être ça :

On choisi un quelconque dans R et on va chercher si, en fonction du y choisi, il existe un (ou des) x dans R tel que g(x)=y. (<- A écrire ABSOLUMENT pour comprendre quel est la "problématique")





Si alors l'équation n'a pas de solution.
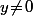
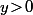
Si alors l'unique solution de est , mais, pour que ce soit effectivement une solution à notre problème, il faut que , c'est à dire , c'est à dire vu que est toujours positif.

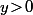
Bilan : Les seuls pour lesquels l'équation admet des solutions sont les et dans ce cas, l'unique solution est .
Donc la fonction , vu comme une fonction de R dans ]0,+oo[ est bijective et sa bijection réciproque est la fonction de ]0,+oo[ dans R définie par .

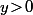
Une fois qu'on sait faire les tableau de variations et les limites, on peut voir voir plus rapidement que g est une bijection de R sur ]0,+oo[, mais bien évidement, lors du calcul de la réciproque, il doit explicitement apparaître à un moment ou un autre qu'on a besoin de la condition pour conclure (sinon, c'est qu'on a fait une erreur de raisonnement)

[LonelyGuy]

@Ben, j'avais oublié de préciser dans l'énoncé c'était avec

[Ben314]

@Ben, j'avais oublié de préciser dans l'énoncé c'était avec

Si effectivement c'est bien ça l'énoncé, alors on s'est franchement fait c.. pour des clous : un malheureux coup d'oeil sur l'expression de g(x) permet de voir qu'il est toujours >0 donc que la fonction g vue de ]0,+oo[ dans [0,1] n'est sûrement pas bijective (il n'y a évidement pas de x tels que g(x)=0)

[LonelyGuy]

Non 0 n'appartient pas à l'intervalle image j'ai dit ça de tête ^^
Elle est bien bijective puisque dans la question ils demandent de le prouver

[mathelot]

elle est bijective de sur