Matrice

[Sheigh]

Bonjour à tous, voici mon exercice :

Soit F1= Ker (A+I) et F2 = Ker((A+I^2)) , avec I3 et
A=
0 0 -1
1 -1 -1
0 1 -2

1- Déterminer F1 et F2.
Je trouve donc F1= vect(1,1,1) et F2 =(1,1,0)

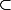
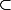
2- A t-on E = vect (1,1,1) F2 ? et F2 F1 ?
Là je me demande quel est E ? Et surtout si on n'a pas deux fois la même question ?

[Pseuda]

Bonjour,

Je ne vois aucune différence entre F1 et F2 dans ton énoncé ...

[FLBP]

Je pense que F2 = Ker((A+I)^2) ...

[aviateur]

Bonjour
Je suis d'accord, Il y a toutes les chances que F_2=Ker[(A+I)^2]
et dans ce cas F_2 est un s.e.v de dimension 2 qui contient F_1 et par ailleurs E c'est F_1.

[Sheigh]

Bonjour,

Vous avez effectivement raison, je me suis trompée dans l'écriture de F2, c'est bien A+I qui est au carré.
Par contre, pouvez-vous m'expliquer comment vous arrivez à dire que F2 est un sev de dimension 2 qui contient F1 et que par ailleurs E est F1 ?
Je vous remercie par avance!

[aviateur]

Bonjour
pour regarde ce que tu as écrit pour !!
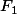
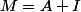
Sinon c'est classique : on pose pour simplifier
on a
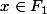
Si cela veut dire que mais alors ; donc
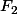
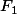
Pour déterminer il faut résoudre l'équation mais tu a oublié les éléments de qui sont dans .

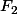
[Sheigh]

D'accord, je comprends un peu mieux.

F2 serait donc vect ((1,1,0),(0,0,1)) ?

Ainsi en réponse à la question E = vect (1,1,1) \subset F2 ? on peut dire oui oui , par contre pour F2 \subet F1, j'aurai plutôt tendance à voire l'inverse c'est à dire F2 \subset F1

[Pseuda]

D'accord, je comprends un peu mieux.

F2 serait donc vect ((1,1,0),(0,0,1)) ?

Ainsi en réponse à la question E = vect (1,1,1) \subset F2 ? on peut dire oui oui , par contre pour F2 \subet F1, j'aurai plutôt tendance à voire l'inverse c'est à dire F2 \subset F1

Bonsoir,

Pour F2, c'est ça. On a .
F2 ne peut pas être inclus dans F1, tout simplement parce qu'un e-v de dim 2 ne peut pas être inclus dans un e-v de dim 1 (tu imagines un plan inclus dans une droite ?). Et par exemple, a-t-on ?

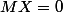
Autre argument : si , alors , donc si , alors .

[Ben314]

Salut,

F2 serait donc vect ((1,1,0),(0,0,1)) ?

Comme l'algèbre linéaire, au début, ça a souvent du mal à rentrer, je t'inciterais plus que fortement à poster ici la façon dont tu t'y prend pour calculer F2 histoire qu'on t'aide / te corrige (avant que tu ne soit "noyé" dans la suite du cours)

[Sheigh]

Bonjour,

Je vous remercie pour vos explications et m'excuse pour mon retard à vous répondre.
Pour le calcul de F2, je m'y prends de la façon suivante :
je calcule A + I que j'élève au carré puis je cherche le ker (A+I)^2 qui est sous la forme d'un système linéaire de 3 équations :
x- y =0
x-y =0
x- y =0
d'où F2 = vect {(1,1,0), (0,0,1)}

3) La question suivante à l'exercice demande si F1 et F2 sont supplémentaires, mais là j'ai un peu de mal à mettre en pratique cette notion, ici.

[Ben314]

Dans un cas pareil, tu n'a rien besoin de savoir concernant la notion de "supplémentaire", à part bien sûr la définition qui est . . .

[Sheigh]

D'accord, alors deux sev de E sont supplémentaires si leur somme est E.
Or E = F1 inclus F2, mais F2 n'inclus pas F1 vu précédemment.
F1+F2 étant le plus petit sev contenant F1 et F2, il ne peut être égal à F2 que si F2 est le plus petit sev contenant F1 et F2 c'est à dire si F2 contient F1. Or on n'a vu précédemment que F2 ne peut pas être dans F1, donc F1 et F2 ne sont pas supplémentaires. Je ne sais pas si je suis claire.