Déterminer deux réels a et b tels que :
1/(k-1)(k+1) = (a/k-1) + (b/k+1).
Svp aidez moi .
j'essaie de rendre au même dénominateur a et b pour ensuite faire une identification mais ça n'a abouti à rien..
Svp j'ai besoin de votre aide.
Merci d'avance!!!
Détermination des réels a et b
3 messages
- Page 1 sur 1
Re: Détermination des réels a et b
Un petit "bonjour", merci. "rendre au même dénominateur  et
et  " n'a aucun sens... Merci d'éviter les multiples "svp, aidez-moi etc", on voit bien que t'as besoin d'aide puisque tu postes dans un forum d'entraide.
" n'a aucun sens... Merci d'éviter les multiples "svp, aidez-moi etc", on voit bien que t'as besoin d'aide puisque tu postes dans un forum d'entraide. 
Pars du membre de droite et réduis au même dénominateur, en supposant différent de
différent de  et
et  , quels que soient
, quels que soient  et
et  :
:
 +b(k-1) }{ (k-1)(k+1) }= \frac{ (a+b)k +a-b}{ (k-1)(k+1) }) .
.
Ainsi, trouver deux réels et
et  tels que pour tout
tels que pour tout  différent de
différent de  et
et  , on ait
, on ait (k+1)} = \frac{ a }{k-1} + \frac{ b}{k+1}) revient à chercher deux réels
revient à chercher deux réels  et
et  tels que pour tout
tels que pour tout  différent de
différent de  et
et  , on ait :
, on ait :
(k+1)} = \frac{ (a+b)k +a-b}{ (k-1)(k+1) }) ,
,
c'est-à-dire quek +a-b=1) . Donc par identification*
. Donc par identification* 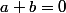 et
et 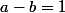 . En résolvant un système de deux équations à deux inconnues tu devrais pouvoir en déduire que
. En résolvant un système de deux équations à deux inconnues tu devrais pouvoir en déduire que 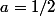 et
et 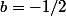 . Je te laisse écrire les détails et conclure.
. Je te laisse écrire les détails et conclure. 
_____________________________________________
* Deux polynômes sont égaux si et seulement si leur coefficient sont égaux donc en voyantk +a-b) et
et 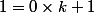 comme deux polynômes en
comme deux polynômes en  ,
, k +a-b=1) si et seulement si
si et seulement si k+a-b=0\times k +1) , c'est-à-dire
, c'est-à-dire 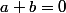 et
et 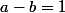 .
.

Pars du membre de droite et réduis au même dénominateur, en supposant
Ainsi, trouver deux réels
c'est-à-dire que
_____________________________________________
* Deux polynômes sont égaux si et seulement si leur coefficient sont égaux donc en voyant
- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 95 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
