Convergence suite
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
kerst
- Membre Naturel
- Messages: 63
- Enregistré le: 13 Nov 2017, 10:36
-
 par kerst » 22 Mar 2018, 11:58
par kerst » 22 Mar 2018, 11:58
bonjour,
je dois étudier la convergence de
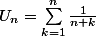
Est-ce que ce raisonnement est correct :
1/2n <= 1/(n+k) <= 1/n
en appliquant la somme on obtient :
1/2<=Un<=1
de plus 1/(n+k)>0 donc Un est croissante
Un est croissante et majorée donc elle converge
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 22 Mar 2018, 12:05
par infernaleur » 22 Mar 2018, 12:05
Salut,
c'est plutôt ça l’inégalité :
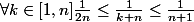
Donc en sommant :
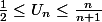
.
Ensuite effectivement
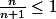
donc ton inégalité final est juste.
Pour la croissance pour bien justifier ce te conseille d'étudier le signe de
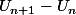
.
-
kerst
- Membre Naturel
- Messages: 63
- Enregistré le: 13 Nov 2017, 10:36
-
 par kerst » 22 Mar 2018, 12:20
par kerst » 22 Mar 2018, 12:20
Pour la croissance j'ai :
}+ \sum_{k=1}^{n}(\frac{1}{n+1+k} - \frac{1}{n+k} ))
Si je développe la somme il me reste à la fin
}-\frac{1}{n+1}+\frac{1}{2n+1}=\frac{1}{2n+1}-\frac{1}{2n+2}>0)
c'est ça?
-
infernaleur
- Membre Irrationnel
- Messages: 1071
- Enregistré le: 20 Avr 2017, 17:45
-
 par infernaleur » 22 Mar 2018, 13:12
par infernaleur » 22 Mar 2018, 13:12
kerst a écrit:Pour la croissance j'ai :
}+ \sum_{k=1}^{n}(\frac{1}{n+1+k} - \frac{1}{n+k} ))
Si je développe la somme il me reste à la fin
}-\frac{1}{n+1}+\frac{1}{2n+1}=\frac{1}{2n+1}-\frac{1}{2n+2}>0)
c'est ça?
Oui
-
kerst
- Membre Naturel
- Messages: 63
- Enregistré le: 13 Nov 2017, 10:36
-
 par kerst » 22 Mar 2018, 13:28
par kerst » 22 Mar 2018, 13:28
merci !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 82 invités