Arithmétique, math spé, polynômes premiers entre eux

[neutrinou]

Bonjour,
On me demande de montrer que pour tout entier n, les entiers 2n^2+10n+13 et n+3 sont premiers entre eux.
Je voudrais savoir si mon raisonnement tient (peu importe qu'il y en ait d'autres plus courts, plus élégants)
Je fais les transformations suivantes sur le premier polynôme :
2 n (n + 3) + 4 n + 13
2 n (n + 3) + 4 n + 12 + 1
2 n (n + 3) + 4 (n + 3) + 1
(n + 3) (2 n + 4) + 1
Si je tente une division euclidienne de ce résultat par n+3, j'obtiens un quotient, (2 n + 4) et un reste 1.
Il est clairement impossible d'aller plus loin quelle que soit la valeur de n. En effet, 1 / (n+3) ne peut donner un entier.
Est-ce que je fais une erreur logique si je dis que j'ai ainsi démontré que ces polynômes étaient premiers ? Y aurait-il une phrase explicative à rajouter ?
Merci de votre aide.
Pascal

[Elias]

Salut, il y a de l'idée mais ça n'est pas rigoureux.
En particulier, tu donnes l'impression de montrer seulement que n+3 ne divise pas 2n^2+10n+13 alors qu'il faut montrer que ces entiers sont premiers entre eux.

Je propose cette façon de rédiger (tu as fais le plus dur en transformant l'expression de 2n^2+10n+13).

On fixe n entier.
Tu as déjà montré que 2n^2+10n+13 = (n + 3) (2 n + 4) + 1
Si un entier d divise simultanément 2n^2+10n+13 et n+3, alors il divisera la combinaison linéaire :
2n^2+10n+13 - (2n+4)(n+3) = 1.

Ainsi, les diviseurs communs de 2n^2+10n+13 et n+3 sont des diviseurs de 1. Ce sont donc exactement -1 et 1 donc pgcd ( 2n^2+10n+13 ; n+3) = 1.

PS: ne parle pas de polynômes premiers entre eux mais d'entiers premiers entre eux (cela a une signification précise que tu ne connais pas encore. De plus, ici il n'y a aucun polynôme (des expressions polynômiales si on veut..)).

[Mimosa]

Bonjour

Le raisonnement est juste. Simplement je ne parlerai pas du tout de polynômes. En fait, tu as fait la division euclidienne de l'entier par 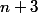et tu as trouvé le reste . Tu peux conclure comme tu l'as fait, ou citer Bézout.

[neutrinou]

Un grand merci à tous les deux !
Bien noté pour les polynômes.
Cool le coup de la variation sur des combinaisons linéaires. Je comprends la richesse du truc, mais je n'arrive pas à bien les utiliser encore, je manque de subtilité. Mais j'ai bon espoir !