Séries numériques

[webosfredo]

Bonjour .
j'ai un ex sur les séries .
J'aimerais connaître votre opinion sur ce que j'écris.

l'énoncé est :

On considère 2 séries:
, , pour




1 Quelle est la nature de chacune de ces séries ?
2 Vérifier l'équivalence de et pour
3 Que déduisez vous des 2 questions précédentes ?

[Elias]

Salut,

pour la 1), je comprends pas trop ce que tu fais. Tu as l'air de connaître le résultat sur les séries alternées mais tu te compliques la vie pour rien.

Une série est alternée si son terme général est de la forme où est une suite de signe constant.
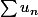
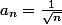
Ici, c'est visiblement le cas pour la série où le terme général est la forme avec définie pour tout par (positive).
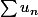
Cette suite tend vers 0 en décroissant donc d'après le théorème des séries alternées, la série est convergente.

Ensuite, il y a une grosse bêtise quand tu écris quecar tu sembles croire que |a+b|=|a|+|b|.

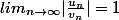
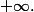
De plus, ce n'est pas parce que que l'on peut conclure que les suiteset sont équivalentes en Il faut une égalité sans valeur absolue. Exemple simple : les suiteset .


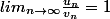
Ensuite, le fait que (pour des suites telles qu'un nombre fini de terme est nul) ne permet pas "d'admettre" que est à peu près égal à pour n grand (comme tu l'écris) mais c'est une des définitions (bien carrée) de équivalent à .

Sinon, ici, on peut dire que pour tout , on a, ce qui devrait permettre de conclure.


Sinon, la dernière phrase est archi fausse car le théorème que tu sembles utiliser ne marche que si les suites sont positives. Ce qui n'est pas le cas ici et c'est justement ceci que l'exercice souhaite mettre en valeur.

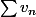
Du coup, il faut réfléchir à la nature de la série (par exemple, tu sais que la somme d'une suite convergente avec une suite divergente donne une suite divergente donc adapte pour les séries).

[webosfredo]

merci trident pour ta réponse.
Donc pour résumer :

dans la première partie je cherchais à démonter que
pour les n pair la suite decroit et a 0 pour limite
pour les n impair la suite croit et a 0 pour limite et que la série converge.

dans la deuxième il faut que je refasse le calcul en gardant tous les termes en pour prouver l'équivalence de u et v

pour le troisième je ne connais pas le théorème qui pourrait s'appliquer l

[Elias]

Pour la 1), tu peux "enlever" la partie "(-1)^n". Le théorème des séries alternées te dit que c'est la suite (1/racine(n)) qui doit tendre vers 0 en décroissant.

Ensuite, si tu veux vraiment montrer pour le plaisir que (-1)^n/ racine(n) tend vers 0, tu peux prendre la valeur absolue (une suite tend vers 0 si et seulement si elle tend vers 0 en valeur absolue).

Pour la 2), je t'ai donné ce que valait le quotient v_n/u_n, il ne reste plus qu'à montrer qu'il tend vers 1, ce qui est direct avec l'expression que j'ai donnée non ?

Ensuite pour la 3), de façon générale, si (x_n) est convergente et (y_n) divergente, alors la suite somme (w_n) définie par w_n = x_n + y_n est divergente car si ce n'etait pas le cas, comme y_n = w_n + (-x_n), on en déduirait (y_n) convergente en tant que somme de deux suites convergentes.


Du coup, c'est pareil pour les series en considérant les suites des sommes partielles à chaque fois.

La sérieest convergente (fraîchement démontré question 1) et la série est divergente (série harmonique) donc notre série est divergente.

Moralité de l'exo: (u_n) et (v_n) sont équivalentes mais les séries ne sont pas de même nature (car justement, ces suites ne sont pas positives (ou de signe constant à partir d'un certain rang pour être plus précis)).