Présentation de groupes

[yakamonéyé]

Bonjour,
Je me suis intéressé à un cours sur les groupes libres et les présentations de groupes, mais n'ai pas tout à fait le niveau nécessaire pour pouvoir correctement l'aborder.

Dans le document suivant, je bloque à deux endroits, les réponses sont probablement évidentes, mais je ne parviens pas à les trouver : http://sma.epfl.ch/~hessbell/topo_alg/PresGrpe.pdf

A la fin de la page 2 : pourquoi (sans faire de raccourci svp) le fait que la propriété universelle des groupes libres nous garantisse l'unicité de l'extension de IdX, implique le résultat qui suit ?

Autre question, à laquelle la réponse est probablement encore plus évidente : page 6, preuve de la proposition 6 : pourquoi est-il clair que N est un sous-groupes normal de F(x) ?

Merci !

[Ben314]

Pour la première question, c'est concon :
Tu regarde le diagramme général définissant la notion de "groupe libre" (celui de la définition du bas de la page 1).
Dans ce diagramme (valable pour tout groupe H et toute application f de X dans H), tu prend H=G et f= et la définition te dit qu'il existe une unique application 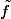de G dans H=G qui fasse commuter le digramme, c'est à dire telle que (vu qu'on a pris f=).
Or, bien évidement, l'application vérifie et comme dans la définition on nous dit qu'une telle application 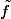est unique, ça signifie que la seule et unique application 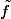de G dans G telle que , c'est .

[yakamonéyé]

Merci beaucoup ! De là, je préfère être sûr de la fin du raisonnement : comme le deuxième diagramme page 2 commute, on a , donc de G dans G est une extension de de X dans G, donc par la propriété d'unicité, on a le résultat. Est-ce juste ? Je n'ai jamais manipulé ni ces théorèmes ni les diagrammes commutatifs.

Et, savez-vous la réponse à ma deuxième question ?

[Ben314]

Oui, c'est bien ça.
Et j'ai la réponse à la deuxième question, sauf que j'ai cours à 16h15 et qu'il est... 16h16
(fin à 17h45)

[yakamonéyé]

Pas de soucis, je ne suis pas à quelques heures près ; c'est déjà généreux de prendre le temps de répondre

[Ben314]

Pour le truc page 6, ça provient simplement du fait que le conjugué d'un produit, c'est le produit des conjugué et du fait que, par définition même, le conjugué d'un élément de la forme (avec ) est de la même forme.
Si tu veut un truc plus calculatoire, si est un élément quelconque de (avec les notation et conventions du poly.) et que est un élement quelconque de alors et c'est bien lui aussi un élément de

[yakamonéyé]

Merci !