Probabilités

[juliepan]

petit problème sur un exercice de probabilité : sujet de concours ecricome série éco (je suis en B/L), merci :

deux personnes A et B partent en vacances de façons indépendantes dans un peys E.
leur séjour dans ce pays peut s'étaler sur n journées (n > 3) numérotées 1,2.....n
pour éventuellement s'y rencontrer, elles ont projeté de séjourner trois jours consécutifs (et trois jours seulement) dans un hôtel H, choisi par elles.
on suppose que les jours d'arrivée possibles 1,2,... n -2 de ces deux personnes dans cet hotel sont deux variables aléatoires uniformes et indépendantes.
les arrivées ont lieu le matin et les départs le soir, deux jours plus tars.

1. (a) Quelle est la probabilité que A et B arrivent le même jour ?

(b) quelle est la probabilité qu'elles arrivent avec un jour d'écart ?

(c) quelle est la probabilité qu'elles puissent se rencontrer dans l'hotel ?

2. sachant que A et B se sont rencontrées, quelle est la probabilité qu'elles ne puissent passer qu'une journée ensemble ??



je ne vois vraiment par où commencer avec ce problème !! :hum:

[BancH]

J'essaie de te montrer pour le 1 mais je suis pas sûr d'avoir bon.

A Quelle est la probabilité que A et B arrivent le même jour ? Si est arrivé le jour , quel est la probabilité pour que arrive le même jour ?

C'est l'inverse du nombre de jours.



B quelle est la probabilité qu'elles arrivent avec un jour d'écart ? Si arrive le jour , quelle est la probabilité pour que arrive le jour 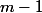ou le jour 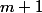? En sachant que si 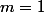alors 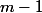n'existe pas et que si 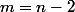alors 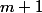n'existe pas.

Là tu prends le nombre de jours: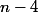 , (on a enlevé les deux cas 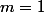et 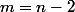), tu multiplies par deux car on a deux cas favorables ( 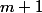et 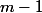), tu ajoutes les deux cas 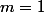et 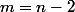et tu divises par le carré du nombre de jours.



C quelle est la probabilité qu'elles puissent se rencontrer dans l'hotel ?On admet que arrive avant ou le même jour que . Si arrive le jour , quelle est la probabilité pour que arrive le jour , le jour 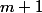ou le jour 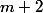sachant que si 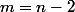, alors 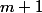et 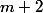n'existent pas et que si 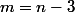, 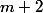n'existe pas.

Nombre de jours où l'on a trois cas favorables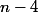 multiplié par trois car on a trois cas favorables, plus 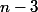multiplié par deux car si 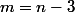alors on a que deux cas favorables, plus 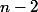(le cas ).
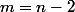On divise le tout par le carré du nombre de jours puis par deux car on a établi un ordre lorsque l'on a dit " arrive avant ".

[alben]

J'essaie de te montrer pour le 1 mais je suis pas sûr d'avoir bon.

B quelle est la probabilité qu'elles arrivent avec un jour d'écart ? Si arrive le jour , quelle est la probabilité pour que arrive le jour ou le jour ? En sachant que si alors n'existe pas et que si alors n'existe pas.

Là tu prends le nombre de jours: , (on a enlevé les deux cas et ), tu multiplies par deux car on a deux cas favorables ( et ), tu ajoutes les deux cas et et tu divises par le carré du nombre de jours.

Bonsoir,
C'est presque ça mais ce n'était pas le carré mais (n-2)(n-3)
On peut faire plus simple : le premier arrivé a (n-2) possibilités. Le second n'a qu'une possibilité. Donc la prob que A arrive un certain jour et B le lendemain est 1/(n-2). Idem pour B le premier et A le second. Au total 2(n-2) :id:

[alben]

Non, j'ai écrit des bétises, tu as raison, le premier n'a qu'une proba de
d'arriver un jour "possible" et ce jour étant fixé, le second n'a plus qu'une possibilité :
au total

[BancH]

Et le reste c'est bon ?

[alben]

En revanche pour le dernier cas, j'arrive à un résultat différent de BancH
je trouve (5n-16)/[(n-2)²] en additionnant (n-2)+2(n-3)+2(n-4) qui sont les cas favorables pour qu'ils arrivent respectivement avec 0,1 ou 2 jours d'écart

[alben]

Pour préciser le dernier résultat on peut énumérer toutes les situations :
A arrive le 1er jour : 3 possibilités pour B
A arrive le 2iéme jour : 4 possibilités pour B
A arrive le 4iéme jour : 5 possibilités pour B
A arrive le 5iéme jour : 5 possibilités pour B
etc

A arrive le (n-4)ième jour : 5 possibilités pour B
A arrive le (n-3)ième jour : 4 possibilités pour B
A arrive le (n-2)ième jour : 3 possibilités pour B

Au total 5(n-6)+3+4+4+3=5n-16
A rapporter aux (n-2)²possibilités

[BancH]

Tu as raison !
C'est parce que j'avais en tête que lorsque augmentait, la probabilité se rapprochait de , alors qu'elle tend en fait vers .

[BancH]

Et pour finir l'exercice:

2. sachant que A et B se sont rencontrées, quelle est la probabilité qu'elles ne puissent passer qu'une journée ensemble ??

a 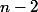plannings différents, supposons que les trois jours de sont déterminés, alors a exactement un jour en commun deux fois sur cinq, 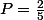sauf si ou , là on a et si ou alors .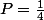

Pour avoir la probabilité totale, il suffit de faire la moyenne des probabilités de chaque jour:

avec

Et si on résonne dans l'autre sens avec les trois jours de déjà déterminés, on a la même probabilité, donc au final on a:

[alben]

Désolé BancH mais ce n'est pas ça pour la fin
Mais comme on ne vas pas faire le boulot de juliepan qui ne prend même pas la peine de participer à la discussion, on en reparlera un peu plus tard :hum:

[BancH]

Ok, on verra quand il se connectera.

[BQss]

petit problème sur un exercice de probabilité : sujet de concours ecricome série éco (je suis en B/L), merci :

deux personnes A et B partent en vacances de façons indépendantes dans un peys E.
leur séjour dans ce pays peut s'étaler sur n journées (n > 3) numérotées 1,2.....n
pour éventuellement s'y rencontrer, elles ont projeté de séjourner trois jours consécutifs (et trois jours seulement) dans un hôtel H, choisi par elles.
on suppose que les jours d'arrivée possibles 1,2,... n -2 de ces deux personnes dans cet hotel sont deux variables aléatoires uniformes et indépendantes.
les arrivées ont lieu le matin et les départs le soir, deux jours plus tars.

1. (a) Quelle est la probabilité que A et B arrivent le même jour ?

(b) quelle est la probabilité qu'elles arrivent avec un jour d'écart ?

(c) quelle est la probabilité qu'elles puissent se rencontrer dans l'hotel ?

2. sachant que A et B se sont rencontrées, quelle est la probabilité qu'elles ne puissent passer qu'une journée ensemble ??



je ne vois vraiment par où commencer avec ce problème !! :hum:

1.a C'est tout simplement [1/(n-2)]^2*(n-2), soit 1/(n-2), tout simplement...
on a utiliser l'inependance des deux variables, l'expression de la loi uniforme et sommé(c'est le "*(n-2)") sur le nombre de jour possible...

b.elementaire a nouveau:
2*(1/(n-2))^2*(n-3)
on multiplie par 2 car c'est ou l'un ou l'autre qui est en avance d'un jour, on met au carré car variable independante, loi uniforme donc 1/(n-2) est la probabilité d'arrivée un jour j et on multiplie par n-3 c'est a dire le nombre de possibilité d'avoir quelqu'un qui arrive un jour n et l'autre un jour n+1.

c.Encore elementaire
Chacun reste trois jours a l'hotel, il suffit qu'ils aient un jour en commun.
2*[1/(n-2)*2/(n-2)*(n-4) +1/(n-2)*1/(n-2)] + [1/(n-2)]^2*(n-2)

C'est à dire la probabilité que l'un arrive au jour j multiplié par la probabilité que l'autre arrive le lendemain ou le surlendemain("2/(n-2)"), on multiplie ca par deux car c'est ou l'un ou l'autre qui est dans cette situation et on multiplie par le nombre de jour ou cela est possible c'est a dire jusqu'a n-4(on traite separement le jour n-3 car a n-3 il n'y a que le lendemain que l'autre peut arriver c'est le "+1/(n-2)*1/(n-2)") et enfin on somme a tout cela la probabilité qu'ils arrivent le meme jour.
On note bien que tout ces evenements sont trivialements incompatibles donc leur reunions est sommable.

2.c'est redondant a force(Il y a beaucoup plus simple que la piste que vous avez emprunté les amis)(PS: il n'y a aucune moyenne a faire sur un probleme portant uniquement sur des probabilités... quand bien même il s'agit de probabilité conditionnelle, utilisé plutot un rapport de mesure... Le nouvel espace de proba etant celui de l'evenement conditionel qu'on suppose réalisé, les evenements sachant n'etant alors rien d'autre que ceux pouvants ce realiser dans ce cadre (A inter B), avec B la condition et A un evenement quelquonque, on mesure alors la masse de A dans B que l'on divise par la masse B pour en avoir un rapport probabiliste P(A inter B)/P(B)):

Ainsi:
Pour qu'il ne reste qu'une journée ensemble, il faut que le deuxieme n'arrive que le le jour du depart du premier, soit son troisieme jour.
Donc:
2*(1/(n-2))^2*(n-4) ca c'est la probabilité qu'il ne reste qu'une journée ensemble on appelle cet evenement I
Et P(R) la probabilité qu'ils se rencontrent dans l'hotel calculé a la question precedente.
Soit donc P(I/R)= P(R INTER I)/ P(R) = P(I) / P(R) Car I C R
et donc:
P(I/R) = 2*(1/(n-2))^2*(n-4) / P(R)

Explication pour I:
Deux fois car soit l'un soit l'autre.
(1/(n-2))^2 la probabilité d'arriver un jour n pour l'un et que l'autre arrive le jour n+2, *(n-4), le nombre de jour ou cela est possible(vu qu'ils ne peuvent arriver au jour "n-1" ou "n" c'est a dire la veille du depart ou le jour meme).

[BQss]

double post

[alben]

Bonjour,

Je n'ai pas vu à quoi tu arrives pour 1c et je suis pas d'accord avec toi non plus pour le 2 qui est effectivement très simple.

Mais je pense qu'il faut attendre que le posteur initial se manifeste avant de continuer à lui fournir la réponse qu'il n'aura qu'à recopier sans même dire merci.
PS tu devrais utiliser latex quand tu utilises des formules un peu compliquées, c'est presque illisible

[juliepan]

ok, merci pr ttes ces indications, jy vois bcp plus clair...
et ca n'ai pas forcément volontaire si je n'ai pas pu participer à la discussion comme je l'aurais voulu !! je vois qu'il y a discordance sur 2 résultats mais je ne recherchait pas la solution au problème mais la méthode pour y parvenir !
merci...

[BQss]

Bonjour,

Je n'ai pas vu à quoi tu arrives pour 1c et je suis pas d'accord avec toi non plus pour le 2 qui est effectivement très simple.

Mais je pense qu'il faut attendre que le posteur initial se manifeste avant de continuer à lui fournir la réponse qu'il n'aura qu'à recopier sans même dire merci.
PS tu devrais utiliser latex quand tu utilises des formules un peu compliquées, c'est presque illisible

Bonjour,

Qu'est ce que tu ne comprends pas dans 1.c?
Quand a 2 (je ne vois pas ou on peut etre en desaccord avec ce que j'ai ecrit, tout est expliqué) ou alors dis moi ou est ce que tu n'es pas d'accord dans la demonstration, que je puisse discuter avec toi...

[alben]

Bonjour,

Qu'est ce que tu ne comprends pas dans 1.c?
Quand a 2 (je ne vois pas ou on peut etre en desaccord avec ce que j'ai ecrit, tout est expliqué) ou alors dis moi ou est ce que tu n'est pas d'accord dans la demonstration, que je puisse discuter avec toi...

En fait je pense qu'on est d'accord, c'est simplement le fait que tes formules sont presques illisibles, je n'avais pas bien vu
Pour le 1c,
Pour le 2

Pour utiliser Latex, il faut taper tes formules comme ceci,
P(I/R) =\frac{P(I)}{P(R)}=\frac{2(n-3)}{5n-16}
selectionner ton texte et utiliser l'outil TEX qui figure dans ta fenêtre, ça donne

[BQss]

En fait je pense qu'on est d'accord, c'est simplement le fait que tes formules sont presques illisibles, je n'avais pas bien vu
Pour le 1c,
Pour le 2

Pour utiliser Latex, il faut taper tes formules comme ceci,
P(I/R) =\frac{P(I)}{P(R)}=\frac{2(n-3)}{5n-16}
selectionner ton texte et utiliser l'outil TEX qui figure dans ta fenêtre, ça donne

Pour Latex merci j'avais regardé apres, c'est plus par fainéantise qu'autre chose, c'est vrai que c'est plus clair pour les autres.

Oui on trouve pareille au c,en simplifiant c'est ce que vaut aussi ma fraction.

Mais on ne trouve pas pareille au 2:
Moi je trouve


La difference entre le -3 et le -4 c'est que tu as compté jusqu'au depart=j-3 (alors que moi j-4) alors que comme ils ne peuvent pas arriver apres j-2, il ne faut pas comptabiliser l'evenement ou le premier arrive a j-3 car le deuxieme arriverait a j-1 pour qu'il ne reste qu'un jour ensemble et ce n'est pas possible d'arriver a j-1... Au final il faut comptabiliser, (n-4) couple d'arrivée et non pas n-3.

[alben]

Oui c'est toi qui as raison, en fait j'ai calculé la proba qu'ils restent 2 jours ensemble

[BQss]

Oui c'est toi qui as raison, en fait j'ai calculé la proba qu'ils restent 2 jours ensemble

Oui tout à fait, ca correspond à ca.