Sinus et cosinus 1 ere S

[Ioat45]

pour moi ca sera ca

[mathelot]

on a besoin des formules de calcul
soient u,v deux nombres

[Ioat45]

je vois pas comment me debrouiller avec u et v
et

[mathelot]

essaye de développer le carré ci-dessus (à l'aide des formules en u et v)

[mathelot]

on va s'attaquer au deuxième carré




d'où

[Ioat45]

d'accord je voyais pas sa comme sa

Ducoup la question est traité mais je reviens sur la question sur laquelle je bloque toujours car j'ai trouvé les angles de chaque triangle mais je vois pas comment trouvé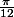

[mathelot]

[mathelot]

Ducoup la question est traitée mais je reviens sur la question sur laquelle je bloque toujours car j'ai trouvé les angles de chaque triangle mais je vois pas comment trouvé

°

[Ioat45]

enfaite la question 1 était très simple

[mathelot]

On n'a pas terminé...il reste le calcul de et

[Ioat45]

exact

[mathelot]

[Ioat45]

sa c'est pour la longueur de AM ou c'est pour le sinus et cosinus?

[mathelot]

sa c'est pour la longueur de AM ou c'est pour le sinus et cosinus?

c'est pour la longueur AM

on calcule et dans le triangle AMJ rectangle en J

Ecris les quotients...

[Ioat45]

Le resultat est celui la mais je les fait à la calculatrice.... comment faire à la main ?

[mathelot]

Le resultat est celui la mais je les fait à la calculatrice.... comment faire à la main ?

Dans le triangle AMJ rectangle en J:

[Ioat45]

[mathelot]

Le resultat est celui la mais je les fait à la calculatrice.... comment faire à la main ?

ces formules sont erronées. les formules exactes sont

[Ioat45]

comment sa erronées ?

[mathelot]