Question de base
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
HelBel
- Messages: 4
- Enregistré le: 01 Mar 2018, 16:29
-
 par HelBel » 01 Mar 2018, 16:35
par HelBel » 01 Mar 2018, 16:35
Bonjour,
Pourriez-vous svp m'expliquer comment affirmer que
^{2} \leq y-x)
Merci par avance pour votre aide,
Hélène
-
mathelot
 par mathelot » 01 Mar 2018, 17:06
par mathelot » 01 Mar 2018, 17:06
Bonjour,
I) déja l'inégalité a du sens si et seulement si

II)
on a l'identité

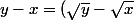(\sqrt{y}+\sqrt{x}))
l'inégalité de départ est équivalente aux inégalités suivantes
-(\sqrt{y}-\sqrt{x})^2 \geq 0)
en factorisant
(\sqrt{y}+\sqrt{x}-\sqrt{y}+\sqrt{x}) \geq 0)
(2\sqrt{x}) \geq 0)
 \geq 0)
ou x=0

ou x=0
la fonction racine étant croissante
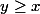
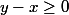
Modifié en dernier par mathelot le 01 Mar 2018, 17:13, modifié 3 fois.
-
HelBel
- Messages: 4
- Enregistré le: 01 Mar 2018, 16:29
-
 par HelBel » 01 Mar 2018, 17:07
par HelBel » 01 Mar 2018, 17:07
Merci pour ton aide Lostounet.
L'objectif de l'exercice au global est de montrer l'uniforme continuité de la fonction racine, et cette question est la première étape.
On a supposé x et y positifs, et 0<x<y
J'avais aussi trouvé "<= x + y" mais le corrigé aboutit à "<= y-x"

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 01 Mar 2018, 17:10
par Lostounet » 01 Mar 2018, 17:10
HelBel a écrit: et 0<x<y
Dans ce cas cela est vrai ! Cf post de Mathelot.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
HelBel
- Messages: 4
- Enregistré le: 01 Mar 2018, 16:29
-
 par HelBel » 01 Mar 2018, 17:23
par HelBel » 01 Mar 2018, 17:23
Merci à tous les deux pour vos réponses si rapides !
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 54 invités