Trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 26 Fév 2018, 23:41
par Hanaconda » 26 Fév 2018, 23:41
Bonsoir tout le monde,
J'ai besoin d'aide pour ces qqs questions, s'il vous plaît:
On pose cos(x-y)/sin(x+y) = (m+1)/(m-1)
Montrer que : m = tan(x+pi/4)tan(y+pi/4)
}{2+cosx} - 2))

Merci beaucoup de bien vouloir m'aider,
bonne soirée.
-
mathelot
 par mathelot » 26 Fév 2018, 23:56
par mathelot » 26 Fév 2018, 23:56
pour le (1)
a) exprime m fonction de cos(x-y) et sin(x+y)
b) développe les expressions
c) divise par cos(x)cos(y) numérateur et dénominateur
d) factorise numérateur et dénominateur
e) utilise
=1)
et
=\frac{tan a + tan b}{1-tan a tanb})
Modifié en dernier par mathelot le 26 Fév 2018, 23:59, modifié 1 fois.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 26 Fév 2018, 23:57
par Lostounet » 26 Fév 2018, 23:57
Hanaconda a écrit:Bonsoir tout le monde,
J'ai besoin d'aide pour ces qqs questions, s'il vous plaît:
On pose cos(x-y)/sin(x+y) = (m+1)/(m-1)
Montrer que : m = tan(x+pi/4)tan(y+pi/4)
}{2+cosx} - 2))

Merci beaucoup de bien vouloir m'aider,
bonne soirée.
Salut,
cos(x-y)/sin(x+y) = (m+1)/(m-1)
=> m cos(x - y) - cos(x-y) = m sin(x + y) + sin(x + y)
Donc
 - sin(x + y)] = sin(x + y) + cos(x - y))
Ensuite, tu peux regarder comment simplifier cos(x - y) - sin(x + y) d'une part et sin(x + y) + cos(x - y) d'autre part. Par exemple cos(x - y) - sin(x + y)
= sin(pi/2 - (x - y)) - sin(x + y))
= sin(p) - sin(q)
= 2 cos( (p + q)/2) sin((p - q)/2)
= 2 cos(pi/4 + y/2) sin(.....)
Tu peux aussi développer les formules de l'énoncé.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 27 Fév 2018, 00:06
par mathelot » 27 Fév 2018, 00:06
Hanaconda a écrit:Bonsoir tout le monde,
J'ai besoin d'aide pour ces qqs questions, s'il vous plaît:
On pose cos(x-y)/sin(x+y) = (m+1)/(m-1)
Montrer que : m = tan(x+pi/4)tan(y+pi/4)
}{2+cosx} - 2)) pas de limite
pas de limite.

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 00:08
par Lostounet » 27 Fév 2018, 00:08
Je ne vois pas de difficultés particulières pour la 2), tel que c'est affiché chez moi c'est pas une forme indéterminée.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 27 Fév 2018, 00:11
par mathelot » 27 Fév 2018, 00:11
Lostounet a écrit:Je ne vois pas de difficultés particulières pour la 2), tel que c'est affiché chez moi c'est pas une forme indéterminée.
idem pour moi
-
mathelot
 par mathelot » 27 Fév 2018, 00:13
par mathelot » 27 Fév 2018, 00:13
pour la (3) on peut écrire

et utiliser
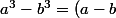(a^2+ab+b^2))

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 00:44
par Lostounet » 27 Fév 2018, 00:44
mathelot a écrit:pour la (3) on peut écrire

et utiliser
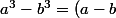(a^2+ab+b^2))
Mais cela permet-il de lever l'indétermination?
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 27 Fév 2018, 00:47
par mathelot » 27 Fév 2018, 00:47
oui
on trouve
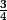
comme limite

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 00:56
par Lostounet » 27 Fév 2018, 00:56
mathelot a écrit:oui
on trouve
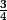
comme limite
Je trouve la même chose mais j'ai utilisé la dérivation... (en fait que sin(x)/x tend vers 1)
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 27 Fév 2018, 01:04
par Hanaconda » 27 Fév 2018, 01:04
J'ai vu les limites trigo usuelles ( sinx/x etc) mais je n'arrive pas vraiment à voir comment vous avez obtenu 3/4 comme limite?
Pour la première limite, devrais-je distinguer deux cas ( quand x>pi et x<pi)?
Et svp, je n'arrive pas vraiment à capter ce que vous m'avez indiqué pour la toute première question.
Merci beaucoup

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 01:13
par Lostounet » 27 Fév 2018, 01:13
Hanaconda a écrit:J'ai vu les limites trigo usuelles ( sinx/x etc) mais je n'arrive pas vraiment à voir comment vous avez obtenu 3/4 comme limite?
Pour la première limite, devrais-je distinguer deux cas ( quand x>pi et x<pi)?
Et svp, je n'arrive pas vraiment à capter ce que vous m'avez indiqué pour la toute première question.
Merci beaucoup
Bon, on va faire petit à petit l ! On ne va pas traiter 3 questions en même temps si tu as du mal déjà avec la première...
Il faut isoler m dans la première équation... Normalement, c'est facile ! Il suffit de faire les produits en croix.
 - cos(x-y) = m sin(x + y) + sin(x + y))
donc:
 - sin(x + y)] = cos(x - y) + sin(x + y))
Donc
 + sin(x + y)}{[(cos(x - y) - sin(x + y)] })
Le numérateur cos(x - y) + sin(x + y) = cos(x - y) + cos(pi/2 - (x + y))
Tu peux essayer les formules cos(p) + cos(q) pour le simplifier...
Le dénominateur aussi...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 27 Fév 2018, 01:27
par Hanaconda » 27 Fév 2018, 01:27
Ah oui! Je vois, je vois. Merci beaucoup!

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 01:29
par Lostounet » 27 Fév 2018, 01:29
Pour le deuxième, la fonction x donne (4 + cos^2(x))/(2 + cos(x)) - 2 est continue en x = pi donc il n'y a aucun problème, la limite est de la forme CONSTANTE/0+ ou Constante/0- donc + ou - infini selon x tend vers pi+ ou pi-.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 27 Fév 2018, 01:36
par Hanaconda » 27 Fév 2018, 01:36
Pour la toute première, je ne vois pas pourquoi je trouve -tan2x..lol

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 01:38
par Lostounet » 27 Fév 2018, 01:38
Quoi tan(2x) ?J'ai pas parlé de tan(2x)...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 27 Fév 2018, 01:41
par Hanaconda » 27 Fév 2018, 01:41
Oui..Mais c'est ce que j'ai obtenu, je dois avoir commis une erreur quelque part..
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 27 Fév 2018, 01:46
par Hanaconda » 27 Fév 2018, 01:46
Qu'en est-il de la deuxième limite, svp?

-
Lostounet
- Membre Légendaire
- Messages: 9665
- Enregistré le: 16 Mai 2009, 11:00
-
 par Lostounet » 27 Fév 2018, 01:52
par Lostounet » 27 Fév 2018, 01:52
cos(x - y) + sin(x + y) = cos(x - y) + cos(pi/2 - (x + y))
Or cos(p) + cos(q) = 2 cos ((p + q)/2) cos((p - q)/2)
En posant p = x - y
q = pi/2 - (x + y)
p+q = x - y + pi/2 - x - y = pi/2 - 2y
p - q = x - y - pi/2 + x + y = 2x - pi/2
Ainsi, cos(p) + cos(q) = 2 cos ((p + q)/2) cos((p - q)/2) = 2 cos(pi/4 - y) cos(x - pi/4)
Même méthode pour le dénominateur...
cos(x - y) - sin(x + y)
= sin(pi/2 - (x - y)) - sin(x + y))
= sin(p) - sin(q)
= 2 cos( (p + q)/2) sin((p - q)/2)
p = pi/2 - (x - y)
q = x + y
p + q = pi/2 - x + y + x + y = pi/2 + 2y
p - q = pi/2 - x + y - x - y = pi/2 -2x
cos(x - y) - sin(x + y) = 2 cos(pi/4 + y) sin(pi/4 - x)
Donc on trouve: [2 cos(pi/4 - y) cos(x - pi/4)]/[2 cos(pi/4 + y) sin(pi/4 - x)] = (cos(pi/4 - y)cos(pi/4 - x))/(cos(pi/4 + y) sin(pi/4 - x)]
Et tu sais que (cos(pi/4 - y)) = sin(pi/2 - (pi/4 - y)) = sin(pi/4 + y) ...
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
-
mathelot
 par mathelot » 27 Fév 2018, 11:14
par mathelot » 27 Fév 2018, 11:14
pour la (1):
+sin(x+y)}{cos(x-y)-sin(x+y)})
on développe:
cos(y)+sin(x)sin(y)+sin(x)cos(y)+cos(x)sin(y)}{cos(x)cos(y)+sin(x)sin(y)-sin(x)cos(y)-cos(x)sin(y)})
on divise haut et bas par cos(x)cos(y):
tan(y)+tan(x)+tan(y)}{1+tan(x)tan(y)-tan(x)-tan(y)})
on factorise:
)(1+tan(y))}{(1-tan(x))(1-tan(y))})
or :
}{1-tan(x)}=\tan(x+\frac{\pi}{4}))
d'où
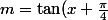\tan(y+\frac{\pi}{4}))
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 87 invités
comme limite