Limites et trigonométrie
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 23 Fév 2018, 21:13
par Hanaconda » 23 Fév 2018, 21:13
Bonsoir,
J'ai une série d'exercices à faire et j'ai du mal à résoudre deux questions qui s'y trouvent. Les voici:
- Montrer que ∀x ∈ ]0,π/2[ : cosx > 1 - x²/2 et déduire que (∀x ∈ ]0,π/3[ ) tanx - sinx < x
- Montrer que ∀x ∈ ]0,π/3[ : tanx < x + x²
Déduire

et

( cela vient après une question demandant de montrer que sinx<x<tanx à l'aide du cercle trigonométrique, j'ai pu la faire. )
Merci beaucoup d'avance,
bonne soirée!
-
pascal16
- Membre Légendaire
- Messages: 6663
- Enregistré le: 01 Mar 2017, 12:58
- Localisation: Angoulème : Ville de la BD et du FFA. gare TGV
-
 par pascal16 » 23 Fév 2018, 21:41
par pascal16 » 23 Fév 2018, 21:41
cosx > 1 - x²/2
tu peux étudier f(x)= cox(x)-(1-x²/2)
deux dérivées pour conclure
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 23 Fév 2018, 21:55
par Hanaconda » 23 Fév 2018, 21:55
Je n'ai pas encore vu la dérivation

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 23 Fév 2018, 22:44
par Pseuda » 23 Fév 2018, 22:44
Bonjour,
x=2*(x/2)>2*sin(x/2)>0, donc x²>4*sin²(x/2)=2*(1-cos(x)), d'où x²/2>1-cos(x) => cos(x)>1-x²/2.
-
mathelot
 par mathelot » 23 Fév 2018, 22:46
par mathelot » 23 Fév 2018, 22:46
on sait que sin x < x < tan x pour

pour

,
les inégalités suivantes sont équivalentes


)
}{\dfrac{x^2}{4}})
la dernière inégalité résulte de

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 23 Fév 2018, 22:50
par Pseuda » 23 Fév 2018, 22:50
@mathelot C'est la même démonstration. Seulement, ce n'est pas du niveau 2nde, comme le reste des questions d'ailleurs. Et je pense qu'il n'y a pas plus simple. Bizarre.
-
mathelot
 par mathelot » 23 Fév 2018, 22:59
par mathelot » 23 Fév 2018, 22:59
pour la question (1)
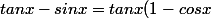 < \sqrt{3} \times \frac{x^2}{2})
car


équivaut à

équivaut à

vraie car

-
mathelot
 par mathelot » 23 Fév 2018, 23:02
par mathelot » 23 Fév 2018, 23:02
Pseuda a écrit:@mathelot C'est la même démonstration. Seulement, ce n'est pas du niveau 2nde, comme le reste des questions d'ailleurs. Et je pense qu'il n'y a pas plus simple. Bizarre.
je pense qu 'elle est en 1ere mais qu'ils n'ont pas encore étudié la dérivation

-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 23 Fév 2018, 23:03
par Hanaconda » 23 Fév 2018, 23:03
Merci beaucoup! Oui, je suis en première. Mais notre programme est différent du français.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 23 Fév 2018, 23:15
par Pseuda » 23 Fév 2018, 23:15
En effet, les élèves français ne font pas ça en 1ère (pour la 1ère question, il faut connaître les formules de duplication des sin et cos, et la fonction tan n'est même pas au programme !!!). Si ce n'est pas indiscret, tu vis dans quel pays ?
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 23 Fév 2018, 23:24
par Hanaconda » 23 Fév 2018, 23:24
Je vis au Maroc. Je m'étonne d'apprendre que nous avons un programme différent du vôtre!
-
mathelot
 par mathelot » 23 Fév 2018, 23:28
par mathelot » 23 Fév 2018, 23:28
Hanaconda a écrit:Je vis au Maroc. Je m'étonne d'apprendre que nous avons un programme différent du vôtre!
En France, on fait le programme: dérivation,trigonométrie, produit scalaire.
La tangente n'est pas au programme mais je suis certain que des profsfrançais l'enseignent.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 23 Fév 2018, 23:29
par Pseuda » 23 Fév 2018, 23:29
C'est normal, ce n'est pas le même programme d'un pays à l'autre. Le programme en France est très en retard, par rapport aux autres pays européens, par rapport aux autres pays francophones, sans parler de l'Asie, qui sont très loin devant nous.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 23 Fév 2018, 23:33
par Pseuda » 23 Fév 2018, 23:33
On parle de la tangente, mais la fonction tangente n'est pas étudiée en tant que telle, même pas en Terminale. Les formules d'addition des sin et cos ne sont vues qu'en Terminale, ainsi que les limites.
Bonne soirée !
-
mathelot
 par mathelot » 23 Fév 2018, 23:36
par mathelot » 23 Fév 2018, 23:36
Pseuda a écrit:On parle de la tangente, mais la fonction tangente n'est pas étudiée en tant que telle, même pas en Terminale. Les formules d'addition des sin et cos ne sont vues qu'en Terminale, ainsi que les limites.
mode apparté ON
est ce que tu sais quelle est la première formule de trigonométrie qui entraine toutes les autres ?
moi, je commence par cos(a-b) dérivée du produit scalaire en Première (je fais du cours particulier)
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 23 Fév 2018, 23:48
par Hanaconda » 23 Fév 2018, 23:48
Pouvez-vous me prêter un coup de main pour la dernière s'il vous plait, ou me mettre sur la piste?
-
mathelot
 par mathelot » 23 Fév 2018, 23:52
par mathelot » 23 Fév 2018, 23:52
Hanaconda a écrit:Pouvez-vous me prêter un coup de main pour la dernière s'il vous plait, ou me mettre sur la piste?
je cherche...
-
mathelot
 par mathelot » 23 Fév 2018, 23:59
par mathelot » 23 Fév 2018, 23:59
Hanaconda a écrit:Pouvez-vous me prêter un coup de main pour la dernière s'il vous plait, ou me mettre sur la piste?

as tu vû la formule

pour |q|<1
-
Hanaconda
- Membre Relatif
- Messages: 163
- Enregistré le: 06 Oct 2015, 18:06
-
 par Hanaconda » 24 Fév 2018, 00:04
par Hanaconda » 24 Fév 2018, 00:04
Non, je ne l'ai pas vue

-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 24 Fév 2018, 11:37
par Pseuda » 24 Fév 2018, 11:37
Bonjour,
- pour 1<=x<pi/3, x<=x², et d'après ci-dessus, tanx <= x+ sinx donc tanx < x+x²
- pour 0<x<1, x²+x-2 < 0, donc après transformation de (1-x²/2)(1+x)-1 :
(1-x²/2)(1+x) > 1 => cosx > 1-x²/2 > 1/(1+x) => 1/cosx < x+1 => tanx < sinx (x+1) < x(x+1)=x+x².
Dans tous les cas, tanx <x+x².
Modifié en dernier par
Pseuda le 24 Fév 2018, 12:41, modifié 1 fois.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 45 invités

