Denombrement
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Nekster
- Membre Naturel
- Messages: 69
- Enregistré le: 03 Nov 2016, 19:16
-
 par Nekster » 13 Fév 2018, 21:28
par Nekster » 13 Fév 2018, 21:28
Bonsoir j'ai un petit soucis avec un exercice:
Il y a 6 clients qui souhaitent aller dormir dans un hotel ayant 4 chambres.
Jusqu'a 6 clients peuvent dormir dans la meme chambre.
Combien y a-t-il de possibilité pour repartir les clients?
D'habitude j'aurais utilisé l'arrangement mais la vu que n<p je ne sais plus trop quoi faire...help pls

-
Al-Kashi
- Membre Relatif
- Messages: 122
- Enregistré le: 18 Oct 2007, 00:14
-
 par Al-Kashi » 13 Fév 2018, 22:16
par Al-Kashi » 13 Fév 2018, 22:16
Bonsoir,
Le nombre de façon de placer p objets indiscernable dans n cases (chaque case pouvant contenir plusieurs objets) est:
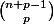
Modifié en dernier par
Al-Kashi le 14 Fév 2018, 11:39, modifié 1 fois.
-
Nekster
- Membre Naturel
- Messages: 69
- Enregistré le: 03 Nov 2016, 19:16
-
 par Nekster » 13 Fév 2018, 22:37
par Nekster » 13 Fév 2018, 22:37
ok merci beaucoups mais pouvez vous m'expliquer le principe de la permutation avec repetition? je pensais que la permutation avec répétition voulait dire,par exemple: Si on considere le mot ELASTIQUE et que l'on cherche le nombre d'anagramme , on utilise la permutation avec repetition et on calcule avec : nb d'anagrammes= 9!/2! (car le E est repeté 2 fois).Je ne vois pas le rapport de cela avec l'exercice de l'hotel

-
Nekster
- Membre Naturel
- Messages: 69
- Enregistré le: 03 Nov 2016, 19:16
-
 par Nekster » 13 Fév 2018, 22:40
par Nekster » 13 Fév 2018, 22:40
Et pourquoi avez vous considéré les clients comment 'objets indiscernable'?Chaque client est unique et la combinaison chambre 1= Julien + sophie n'est pas la meme que la combinaison qui implique chambre 1 = Julien+Stephan non?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 13 Fév 2018, 23:11
par Pseuda » 13 Fév 2018, 23:11
Bonsoir,
Chacun des 6 clients a le choix entre 4 chambres, et les choix sont indépendants. Cela fait 4^6 possibilités. Ou encore, c'est le nombre d'applications d'un ensemble de 6 éléments dans un ensemble de 4.
-
Al-Kashi
- Membre Relatif
- Messages: 122
- Enregistré le: 18 Oct 2007, 00:14
-
 par Al-Kashi » 14 Fév 2018, 11:38
par Al-Kashi » 14 Fév 2018, 11:38
Bonjour,
Il n'y a pas de lien direct avec ta question mais je voulais juste te rappeler la notion de combinaison sans répétition.
Sinon, pour répondre à ta question, il y a
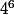
possibilités.
C'est le nombre d'applications d'un ensemble de 6 éléments dans un ensemble de 4 éléments.
Bonne journée
-
beagle
- Habitué(e)
- Messages: 8746
- Enregistré le: 08 Sep 2009, 14:14
-
 par beagle » 14 Fév 2018, 11:54
par beagle » 14 Fév 2018, 11:54
oui, et six clients qui dorment dans la même chambre,
soit on s'éloigne de la réalité,
soit on habitue les gens à faire des economies
soit ...
L'important est de savoir quoi faire lorsqu'il n' y a rien à faire.
-
Al-Kashi
- Membre Relatif
- Messages: 122
- Enregistré le: 18 Oct 2007, 00:14
-
 par Al-Kashi » 14 Fév 2018, 12:46
par Al-Kashi » 14 Fév 2018, 12:46
Tout dépend de la superficie de la chambre

-
Nekster
- Membre Naturel
- Messages: 69
- Enregistré le: 03 Nov 2016, 19:16
-
 par Nekster » 15 Fév 2018, 19:13
par Nekster » 15 Fév 2018, 19:13
desolé pour le retard et merci
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités

