Fonction et dérivabilité

[o2pubcy9]

Bonjour je coince par apport à une question pouvez-vous m'aider svp ?^
j'ai la fonction (x^2)*cos(1/x)+(x/pi)
comment je peut montrer que cette fonction est dérivable sur R* et comment je peut dire qu'elle est prolongeable sur R svp ? J'ai dit que cette fonction est le produit de fonction dérivable mais si je fait le taux d'accroissement je suis coincé...
Ensuite j'ai déduis des question précédentes xn=1/((2n-1)pi) et yn=1/(2npi)
mais comment je peux étudier le signe de f(xn)-f(yn) svp ?

[mathelot]

pour la fonction est dérivable en comme composée de fonctions dérivables.
En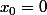 on pose f(0) = 0 Montrer que le prolongement de f est continue en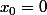
Pour la dérivabilité du prolongement , étudier la limite en x=0 de


remarque: cette fonction est dérivable en x_0=0 bien que sa fonction dérivée n'ait pas de limite en x_0=0

[o2pubcy9]

merci de m'aider svp pour une question on me demande
f qui va de I dans R avec I un intervalle
j'ai une fonction f de classe C1 donc f est dérivable et sa dérivée est continue mais si f'(a)>0 si je veux montrer que f est strictement croissante sur un voisinage de a
je peux prendre a et b appartenant à I et comme f est dérivable par le taux d'accroissement f(b)-f(a)>0 donc f(b)>f(a) donc f est strictement croissante sur un voisinage de a ?

[Elias]

Non,

La fonction f' est continue en a et f'(a) > 0 donc il existe un voisinage V de a tel pour tout x dans V, f ' (x) > 0.

Ainsi, dans ce voisinage, f ' est strictement positive donc f est strictement croissante.

Pour montrer l'existence de V:
C'est un grand classique.
Ecris la définition de la continuitéde f ' en a pour trouver ce voisinage V.
Ce qui doit guider ta preuve " f ' est continue en a donc les f ' (x) sont proches de f ' (a) quand x est proche de a. Mais à un moment (en prenant x suffisament proche de a), ils sont tellement proches de f ' (a) qu'ils sont forcément eux même strictement positifs (car f ' (a) > 0)"

[o2pubcy9]

Bonjour et merci
je vais donc procéder ainsi...
avec des questions précédentes sur les suites rationnelles je trouve
xn=1/((2n-1)pi) et yn=1/(2npi)
mais comment je peux étudier le signe de f(xn)-f(yn) svp ?
quand je calcul f(xn)-f(yn) je trouve ((cos(2npi)+1)/2npi^2)-((cos(2npi)-1)/(2n-1)^2pi^2) *
pour étudier le signe je dois peut être faire une disjonction de cas si n est pair et si n est impart car cos(2n*pi)=1 ou -1 suivant la parité de n...

[Elias]

(les suites (xn) et (yn) sont justement irrationnelles)

Sinon, je sais pas comment t'arrives à ça.
D'ailleurs, n'as tu pas oublié le "x/pi" dans l'expression de f ?

cos ( x+2npi) = cos(x) pour tout x réel et pour tout entier n donc il n'y a pas à dinstinguer les cas pairs ou impairs.

Par exemple, cos( (2n-1)pi) = cos(2npi - pi) = cos(-pi) = -1.

Donc tous les cos vont disparaître.
En utilisant ceci, et en simplifiant tout, je trouve (sauf erreur) que



Cette expression est négative (le numérateur a un discriminant négatif donc est de signe constant et en l'occurence positif).

[mathelot]

Non,

La fonction f' est continue en a et f'(a) > 0 donc il existe un voisinage V de a tel pour tout x dans V, f ' (x) > 0.

Ainsi, dans ce voisinage, f ' est strictement positive donc f est strictement croissante.

Pour montrer l'existence de V:
C'est un grand classique.
Ecris la définition de la continuitéde f ' en a pour trouver ce voisinage V.
Ce qui doit guider ta preuve " f ' est continue en a donc les f ' (x) sont proches de f ' (a) quand x est proche de a. Mais à un moment (en prenant x suffisament proche de a), ils sont tellement proches de f ' (a) qu'ils sont forcément eux même strictement positifs (car f ' (a) > 0)"

un intervalle (i.e un voisinage connexe)

[Elias]

Oui bien sûr, même si c'etait sous entendu, il faut bien le préciser.