Résolu Merci !
4 messages
- Page 1 sur 1
Résolu Merci !
par fioldodidi » 03 Jan 2018, 00:41
Résolu Merci !
Modifié en dernier par fioldodidi le 12 Jan 2018, 23:31, modifié 1 fois.
Re: Distributions et fonctions tests
par Ben314 » 03 Jan 2018, 12:07
Salut,
\!-\!\int\! a_{n}(x)\phi(x)\,dx \right|<br />=\left|\phi (0)\int\! a_{n}(x)\,dx\!-\!\int\! a_{n}(x)\phi(x)\,dx \right|<br />=\left|\int\! a_{n}(x)\big(\phi (0)\!-\!\phi(x)\big)\,dx \right|<br />\leq\int\! a_{n}(x)\left|\phi (0)\!-\!\phi(x)\right|dx)
Or, vu le support de
, on a \left|\phi (0)\!-\!\phi(x)\right|dx=\int_{-\epsilon_n}^{\epsilon_n}\! a_{n}(x)\left|\phi (0)\!-\!\phi(x)\right|dx)
Et, sur l'intervalle)
, on a \!-\!\phi(x)\right|\!\leq b\!)
donc \left|\phi (0)\!-\!\phi(x)\right|dx\leq b\int_{-\epsilon_n}^{\epsilon_n}\! a_{n}(x)\,dx=b)
Or, vu le support de
Et, sur l'intervalle
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Distributions et fonctions tests
par fioldodidi » 11 Jan 2018, 06:46
Merci, j'ai vraiment perdu les réflexes !
Je bloque sur la suite aussi
On pose = \int_{-\infty}^{x}{\rho_{n}(t)})
avec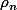 
une suite régularisante.
Je dois comparer les limites de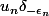
et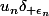 
.
Merci encore.
Je bloque sur la suite aussi
On pose
Je dois comparer les limites de
Merci encore.
Re: Distributions et fonctions tests
par aviateur » 12 Jan 2018, 00:23
Bonjour
Je suppose que ta suite régularisante a pour support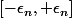
Soit
un fonction test:
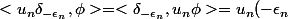 \phi(-\epsilon_n)=0\times \phi(-\epsilon_n)=0)
. Donc =0)
De façon analogue, en remarquant que=1)
tu trouveras que
=\delta_0)
Je suppose que ta suite régularisante a pour support
Soit
De façon analogue, en remarquant que
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :