Bonjour,
Reprenons tout cela alors :
L'ensemble des majorants, c'est
l'ensemble de tous les nombres réels plus grands que ceux qui figurent dans ton ensemble de départ. Si j'appelle M l'ensemble des majorants et E l'ensemble considéré, alors

La borne supérieure est le plus petit des majorants, c'est le plus petit élément de ton ensemble M.
La différence entre borne supérieure et plus grand élément est infime :
le plus grand élément fait partie de l'ensemble que tu regardes, alors que la borne supérieure, pas forcément.
Prenons par exemple
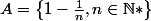
. On peut montrer que l'ensemble des majorants de cet ensemble est
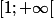
, et donc, le plus petit des majorants, 1, est la borne supérieure de l'ensemble A. Seulement, 1 n'appartient pas à l'ensemble A, ce n'est donc pas le plus grand élément de A.
Note bien d'ailleurs qu'
il n'existe pas forcément de plus grand élément dans un ensemble. En revanche, pour les sous-ensembles de réels, il existe toujours une borne supérieure (quitte à ce que celle-ci vaille l'infini...)
En changeant les" majorants" en "minorants", les "plus grand que" en"plus petit que" et vice versa, tu auras la même chose pour les minorants.
Pour ton exercice, tu dois donc essayer d'encadrer le plus finement possible tes ensembles : entre quel réel a et quel réel b sont compris tous les réels de l'ensemble A ? Une fois que tu as trouvé de tels réels, peux-tu faire encore mieux ? Si non, tu as les deux bornes supérieures et inférieurs.
Ces deux éléments sont-ils dans l'ensemble A ? Si oui, ce sont les plus grands ou plus petits éléments. Sinon, rien de plus.
Les chemins à emprunter pour trouver de tels réels varient évidemment suivant les consignes, mais l'idée est là. J'espère t'avoir aiguillé !

