[Résolu]Endomorphisme et vecteurs propres
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
pierre33
- Membre Naturel
- Messages: 12
- Enregistré le: 06 Jan 2018, 23:22
-
 par pierre33 » 06 Jan 2018, 23:37
par pierre33 » 06 Jan 2018, 23:37
Bonjour à tous,
j'aurais besoin d'aide pour un exo.
1) f désigne un endomorphisme de 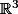 tel que :
tel que :
\Rightarrow (f(V)=V)\\ (V\in D)\Rightarrow (f(V)=-V))
Cette définition fait-elle apparaître des valeurs propres de f ? Quels sont les sous-espaces propres associés ? Les valeurs propres sont 1 et -1. Mais je ne vois pas comment trouver les sous-espaces propres.
J'avais pensé à
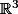
pour le SEP associé à 1.
Si jamais vous pouviez me donner une indication.
Merci d'avance.
Modifié en dernier par
pierre33 le 08 Jan 2018, 16:33, modifié 4 fois.
-
Kolis
- Membre Relatif
- Messages: 482
- Enregistré le: 25 Sep 2015, 16:29
-
 par Kolis » 07 Jan 2018, 09:07
par Kolis » 07 Jan 2018, 09:07
Bonjour !
Si

désignent des supplémentaires dans

tu as les sous espaces propres cherchés.
Sinon, il faudrait nous en dire plus dans ton énoncé.

-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
 par Ben314 » 07 Jan 2018, 11:23
par Ben314 » 07 Jan 2018, 11:23
Salut
pierre33 a écrit:Les valeurs propres sont 1 et -1. Mais je ne vois pas comment trouver les sous-espaces propres.
Comme "indication", ce que je peut te dire, c'est que même ça, c'est faux : si P et D sont vides ou bien égaux à {(0,0,0)} alors les deux affirmations sont forcément vraies et ne disent rien sur les valeurs propres de f.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
pierre33
- Membre Naturel
- Messages: 12
- Enregistré le: 06 Jan 2018, 23:22
-
 par pierre33 » 07 Jan 2018, 12:30
par pierre33 » 07 Jan 2018, 12:30
Bonjour à vous,
merci pour vos réponses.
Je n'ai absolument aucune information sur P et D, c'est bien ce qui me dérange aussi.
En imaginant que P et D soient supplémentaires, comment je trouve les sous espaces propres ?
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 07 Jan 2018, 13:26
par Pseuda » 07 Jan 2018, 13:26
Si P et D sont supplémentaires, f est visiblement la symétrie par rapport à P parallèlement à D.
-
pierre33
- Membre Naturel
- Messages: 12
- Enregistré le: 06 Jan 2018, 23:22
-
 par pierre33 » 07 Jan 2018, 13:44
par pierre33 » 07 Jan 2018, 13:44
D'accord, je n'ai rien compris.
C'est une annale que j'essaie de faire, le cours a du changé. Je n'ai surement pas les bases nécessaires.
Tant pis, sujet clos.
-
Pseuda
- Habitué(e)
- Messages: 3222
- Enregistré le: 08 Avr 2015, 12:44
-
 par Pseuda » 08 Jan 2018, 08:58
par Pseuda » 08 Jan 2018, 08:58
Bonjour,
Dommage. Tu as dû voir que de manière générale, si P et D sont supplémentaires, f est entièrement déterminée par sa restriction à P et sa restriction à D.
Ici, dans une base formée de vecteurs d'une base de P et d'une base de D, la matrice de f est diagonale et sa diagonale ne comporte que des 1 et -1, donc ses valeurs propres sont 1 et -1, et les sous-espaces propres associés sont P et D.
-
pierre33
- Membre Naturel
- Messages: 12
- Enregistré le: 06 Jan 2018, 23:22
-
 par pierre33 » 08 Jan 2018, 16:13
par pierre33 » 08 Jan 2018, 16:13
Bonjour !
Pseuda a écrit:Dommage. Tu as dû voir que de manière générale, si P et D sont supplémentaires, f est entièrement déterminée par sa restriction à P et sa restriction à D.
Justement non ... Je suis en licence physique et notre cours d'algèbre linéaire est assez basique.
En tout cas grâce à vous c'est bon, je pense avoir enfin compris... Il fallait utiliser une info' d'une question précédante qui parlait d'un plan vectoriel et d'une droite vectorielle (ici P et D a priori).
Je trouve alors
=\begin{pmatrix}<br />1 & 0 &0 \\ <br /> 0& 1& 0\\ <br /> 0&0 &-1 <br />\end{pmatrix})
, où B' est une base de l'exercice.
C'est cohérent avec ce que vous me dites, et avec la suite.
Merci encore.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 29 invités
