Bonjour
Sauf si j'ai mal lu (on ne voit pas parfaitement) l'exercice 1 me semble faux.
En effet il suffit de prendre N=1, A=(1) (elle est s.d.p définie positive) , f(x)=x^3 (qui vérifie les hypothèses)
L=lambda=1 , b_1==b1=1/sqrt(3) , alpha_1=1
L'équation est alors h(u)=u-f(u)-1=0=1. alpha_1=1
L'équation est alors
=-\dfrac{1}{\sqrt{3}}+u-u^3=0)
qui admet une unique solution -1.21463.
Mais je prendre u_0=0 qui vérifie |u_0|<a quelque soit a
on a
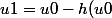/h'(u0)=\dfrac{1}{\sqrt{3}})
Mais
=0)
, u_2 n'est pas défini, la méthode de Newton pose bien problème.
Avec N=2 je suis sûr que l'on peut fabriquer des contre exemples.
Où alors il y a quelque chose que je n'ai pas vu dans les hypothèses

