chalelu a écrit:On peut la déduire en fonction "des coordonnées" (
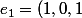)
et
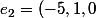)
) ? Dans ce cas comme il y a trois coordonnées, le sous-espace vectoriel est de dimension 3 ?
Attention, par exemple si je prend l'espace vectoriel

(c'est-à-dire l'espace vectoriel constitué du vecteur nul de

), on a
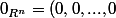)
(où il y a n zéros) pourtant dim E=1 et on a pas dim E=n.
Pour moi la dimension d'un espace vectoriel c'est le nombre d'éléments que contient UNE base de cette espace vectoriel (attention il n'y a pas unicité de la base !). Voila quelques bases élémentaires que tu dois connaître :
*** Par exemple tu as vu qu'une base de

est la base canonique
)
où on pose
,...,e_n=\left(\begin{array}{c}0 \\\vdots \\1\end{array} \right))
.
Cette base est constitué de n vecteurs
)
donc

est de dimension n.
*** Pareil pour la base canonique des polynômes par exemple, tu as du voir que
)
est une base de
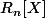
. Comme il y a n+1 éléments (et non n) dans cette base, alors la dimension de
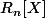
est n+1.
*** Ou encore une base des matrices taille p*q est constitué des matrices élémentaires
_{1 \leq i \leq p,1 \leq j \leq q)
où il y a un 1 dans la ligne i et la colonne j et des 0 partout ailleurs. Tu as

vecteurs dans la base formé des matrices élémentaires ( comme ton i varie de 1 à p tu as p possibilités et pour j tu as q possibilités). Donc tu en déduis que la dimension des matrices de taille p*q est

.
Bref dans ton cas F est engendré par deux vecteurs (que j'ai décidé d'appeler
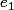
et
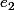
, c'était pas forcément la meilleur notation car on peut confondre avec la notation de la base canonique de
)
Tu peux facilement montrer que la famille
)
est libre sa sera donc une base.
Donc une base de F est constitué de deux vecteurs, on a donc

[merci de me corriger si j'ai dis des conneries]

