Plan complexe
Réponses à toutes vos questions de la 2nde à la Terminale toutes séries
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 15:47
par Anonymous2016 » 13 Déc 2017, 15:47
Bonjour, j'aurai besoin d’être guidé pour cet exercice.

Le début est correct? merci
Modifié en dernier par
Anonymous2016 le 13 Déc 2017, 16:04, modifié 1 fois.
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 13 Déc 2017, 16:12
par Carpate » 13 Déc 2017, 16:12
Oui
Variante :
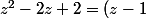^2+1=(z-1)^2-(-1)= (z-1)^2 -i^2=(z-1-i)(z-1+i))
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 17:22
par Anonymous2016 » 13 Déc 2017, 17:22
2) c)

cette réponse est fausse, je suis entrain de la corriger
Modifié en dernier par
Anonymous2016 le 13 Déc 2017, 18:07, modifié 1 fois.
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 17:34
par Anonymous2016 » 13 Déc 2017, 17:34
2)d) comment en déduire la nature du triangle merci? comment on en déduit que le triangle ACD est rectangle?
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 13 Déc 2017, 18:38
par Carpate » 13 Déc 2017, 18:38
Quand tu auras corrigé ton résultat de la question 2-c (réponse Z= 4i), ta réponse à 2-d sera évidente
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 18:47
par Anonymous2016 » 13 Déc 2017, 18:47
j'ai donc trouvé 2i pour la question 2)d) mais je vois pas en quoi c'est évident pour la suite
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 13 Déc 2017, 18:51
par Carpate » 13 Déc 2017, 18:51
Quel est l'argument de Z (qui vaut 4i et non 2i) ?
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 18:57
par Anonymous2016 » 13 Déc 2017, 18:57
je ne comprends pas
-
Carpate
- Habitué(e)
- Messages: 3930
- Enregistré le: 05 Jan 2012, 18:05
-
 par Carpate » 13 Déc 2017, 19:10
par Carpate » 13 Déc 2017, 19:10
Z est un nombre complexe de module ... et dont un argument est ...
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 19:53
par Anonymous2016 » 13 Déc 2017, 19:53
L'argument est l'angle en radian (vecteur u, vecteur OM) ?
Le module |z| est la distance OM (entre l'origine et le point)
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 19:58
par Anonymous2016 » 13 Déc 2017, 19:58
à la 2)c) j'ai trouvé 2i

-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 20:44
par Anonymous2016 » 13 Déc 2017, 20:44
pour la e), par "expliquer la construction effectuée" ils attendent quoi? je comprends pas bien, merci
-
annick
- Habitué(e)
- Messages: 6291
- Enregistré le: 16 Sep 2006, 09:52
-
 par annick » 13 Déc 2017, 21:13
par annick » 13 Déc 2017, 21:13
Tu vas utiliser tes réponses précédentes :
Z=4i=4e^(i pi/2)
De plus, comme Z=(zD-zA)/(zC-zA), cela veut dire que :
Module Z=AD/AC et argument de Z=Angle (AC,AD) (avec des vecteurs pour AC et AD)
Donc :
AD/AC=4, soit AD=4AC
Angle (AC,AD) =pi/2
A partir de là, tu peux facilement construire le point D si tu connais déjà les points A et C.
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 21:21
par Anonymous2016 » 13 Déc 2017, 21:21
dans notre cours, on a pas vu les nombres complexes avec la forme exponentielle. Il n'y a pas une autre méthode? et j'ai trouvé Z=2i, je ne vois pas où est mon erreur
-
danyL
- Membre Rationnel
- Messages: 682
- Enregistré le: 03 Jan 2015, 13:29
-
 par danyL » 13 Déc 2017, 21:36
par danyL » 13 Déc 2017, 21:36
(edit)
Modifié en dernier par
danyL le 13 Déc 2017, 21:54, modifié 1 fois.
-
Anonymous2016
- Membre Naturel
- Messages: 52
- Enregistré le: 15 Oct 2016, 13:27
-
 par Anonymous2016 » 13 Déc 2017, 21:43
par Anonymous2016 » 13 Déc 2017, 21:43
j'ai utilisé la formule
(x-yi)=x^2+y^2)
, il faut donc utiliser les identités remarquables?
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 80 invités


