Combinatoire/Graphs
Réponses à toutes vos questions après le Bac (Fac, Prépa, etc.)
-
Gexo
- Membre Naturel
- Messages: 14
- Enregistré le: 02 Déc 2017, 21:47
-
par Gexo » 02 Déc 2017, 22:00
Bonjour,
Pour ce premier message que je poste sur ce forum, je souhaiterais solliciter une aide concernant un problème de combinatoire/graphs qui m'échappe.
Soient deux ensembles disjoints
et
tels que tout point de
est connecté à un nombre constant
de points de
, et tout point de
est connecté à un nombre constant
de points de
. On appelle
la cardinalité de
et
la cardinalité de
.
(en particulier, noter que
).
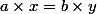
Soit un sous-ensemble
(on notera
sa cardinalité); je souhaiterais connaître le nombre total de points de
auquel cet ensemble
est connecté.
(Le nombre d'arêtes entre
et
est bien entendu
; la difficulté est que plusieurs de ces arêtes, en général, sont connectées à des mêmes points de
).
En vous remerciant pour votre attention et votre aide,
Gexo.
-
Ben314
- Le Ben
- Messages: 21709
- Enregistré le: 11 Nov 2009, 21:53
-
par Ben314 » 02 Déc 2017, 22:33
Salut,
Sans hypothèses supplémentaires, tu va pas pouvoir dire grand chose, à part de vagues inégalités évidentes :
- C'est clairement au moins égal à
et c'est effectivement égal à ça si s=x par exemple, mais il peut y avoir d'autres cas.
- C'est tout aussi clairement au plus égal à
et c'est effectivement égal à ça si s=1 par exemple, mais il peut y avoir d'autres cas.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
-
Gexo
- Membre Naturel
- Messages: 14
- Enregistré le: 02 Déc 2017, 21:47
-
par Gexo » 02 Déc 2017, 23:57
Ben314 a écrit:Salut,
Sans hypothèses supplémentaires, tu va pas pouvoir dire grand chose, à part de vagues inégalités évidentes :
- C'est clairement au moins égal à
et c'est effectivement égal à ça si s=x par exemple, mais il peut y avoir d'autres cas.
- C'est tout aussi clairement au plus égal à
et c'est effectivement égal à ça si s=1 par exemple, mais il peut y avoir d'autres cas.
Bonsoir Ben314,
Merci pour ta réponse; il me semblait que le problème était bien "ficelé" et que, aux connexions à l'intérieur de
et de
près, qui ne nous intéressent pas, on ne peut toujours assigner qu'un seul graph à un ensemble
)
. Qu'en particulier, seule la cardinalité de
importe.
Pour un graph donné, appelons
)
le nombre de connexions entre
et
. Le problème pose des difficultés telles que celle-ci : à partir d'un certain
, tous les points de
sont atteints. Par exemple
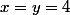
et
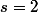
. Alors
=2)
,
=3)
et
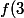=f(4)=4)
.
-
Gexo
- Membre Naturel
- Messages: 14
- Enregistré le: 02 Déc 2017, 21:47
-
par Gexo » 03 Déc 2017, 13:19
Ben314 a écrit:Salut,
Sans hypothèses supplémentaires, tu va pas pouvoir dire grand chose, à part de vagues inégalités évidentes :
- C'est clairement au moins égal à
et c'est effectivement égal à ça si s=x par exemple, mais il peut y avoir d'autres cas.
- C'est tout aussi clairement au plus égal à
et c'est effectivement égal à ça si s=1 par exemple, mais il peut y avoir d'autres cas.
Bonjour Ben314,
C'est bon, j'ai enfin compris ce que tu disais; effectivement, cela ne dépend pas uniquement de la cardinalité de
; en général on ne peut rien dire en effet. Par exemple avec
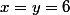
et
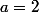
, on peut choisir
tel que
ou
.
Il n'y a donc pas de résultat tel quel.
Merci pour ton aide, bonne journée,
Gexo.
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 36 invités
