Théorème des valeurs intermédiaires avec suites

[Hm50]

Bonsoir à tous. J'ai un DM à rendre pour mercredi et je bloque sur deux questions d'un exercice qui le voici: 
On considère une fonction continue sur [0;+oo[. On donne ci dessous le tableau de variation de f. 
x      0    2    +oo 
                1 
              /  \ 
            /      \ 
f(x) 0          0 
Soit n un entier naturel supérieur ou égal à 2. 
1. Montrer que l'équation f(x)= 1/n admet 2 solutions notées Un et Vn appartenant respectivement aux intervalles ]0;2[ et ]2;+oo[ 
2. Montrer sur la suite (Un) est décroissante. Que peut on en déduire? 
3. Étudié le comportement de la suite (Vn)  lorsque n tend vers +oo. 
Pour la 1 pas de problème c'est à partir du 2 que je bloque. J'ai essayé de faire Un+1-Un mais sans succès. Un grand merci pour toute aide.

[capitaine nuggets]

Salut !

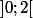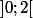est solution sur de l'équation et est solution sur de l'équation .
Donc autrement dit, et .

Compare donc avec (plus grand ou plus petit).
Quel est la monotonie de sur ?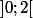
Déduis-en alors si est plus grand ou plus petit que .