Intégrale de surface
14 messages
- Page 1 sur 1
Intégrale de surface
Bonjour,
je n'arrive pas à savoir comment l'on résout un exercice.
J'ai effectué l'intégrale en deux étapes: I=I1+I2
avec: I1 (0,0) à (pi,0)
x:0 à pi
y: 0 à 0 ==>dy=0
I1=-1
I2 (pi,0) à (pi,pi)
x: pi à pi ==> dx=0
y:0 à pi
I2=0
I=-1
Mais je ne sais pas si la méthode est bonne... Si quelqu'un pouvait m'expliquer cela. Merci d'avance !
Re: Intégrale de surface
Bonjour Je ne vois pas de méthode, c'est du chinois, je n'y comprends rien!
Fais un dessin de ton triangle D et tu dois voir que "si tu balayes D pour x allant de 0 à alors pour x fixé y va de zéro à x"
alors pour x fixé y va de zéro à x"
donc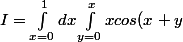 dy=)
Il reste à calculer.
Fais un dessin de ton triangle D et tu dois voir que "si tu balayes D pour x allant de 0 à
donc
Il reste à calculer.
Re: Intégrale de surface
Bonjour,
je suis d'accord "si tu balayes D pour x allant de 0 à pi alors pour x fixé, y va de 0 à x". Cependant je ne comprends pas pourquoi on a alors I= l'intégrale que vous avez mentionné.
Merci
je suis d'accord "si tu balayes D pour x allant de 0 à pi alors pour x fixé, y va de 0 à x". Cependant je ne comprends pas pourquoi on a alors I= l'intégrale que vous avez mentionné.
Merci
Re: Intégrale de surface
Salut,
Ton domaine , c'est l'ensemble des
, c'est l'ensemble des \!\in\!\R^2) tels que
tels que  donc tu peut calculer
donc tu peut calculer \,dx\,dy)
- Soit en l'écrivant sous la forme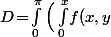\,dy\Big)dx) :
:  varie de 0 à
varie de 0 à  puis, pour chaque
puis, pour chaque  fixé,
fixé,  varie de 0 à
varie de 0 à  .
.
- Soit en l'écrivant sous la forme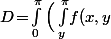\,dx\Big)dy) :
:  varie de 0 à
varie de 0 à  puis, pour chaque
puis, pour chaque  fixé,
fixé,  varie de
varie de  à
à  .
.
Ton domaine
- Soit en l'écrivant sous la forme
- Soit en l'écrivant sous la forme
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Intégrale de surface
Bonjour Oui c'est ça c'est pas 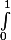 mais
mais  que je voulais écrire et puis
que je voulais écrire et puis  dy) dx) s'écrit parfois
s'écrit parfois
 dy) c'est ce j'ai fait pour éviter des ( )
c'est ce j'ai fait pour éviter des ( )
Re: Intégrale de surface
Avant de lire vos messages, je suis parti sur le changement de variables u=x+y, v=x-y mais finalement ça donne un calcul plus long que celui que vous proposez en restant avec x et y, à condition de commencer par intégrer suivant y.
Avec les deux méthodes, je trouve le même résultat, ce qui est rassurant (mais ne prouve rien).
Avec les deux méthodes, je trouve le même résultat, ce qui est rassurant (mais ne prouve rien).
Re: Intégrale de surface
Jason a écrit:Je trouve I=(-1/2)*pi-2 ?
Salut
Mets ton calcul; il y a un souci quelque part.
Re: Intégrale de surface
voici mon calcul
- Fichiers joints
-
- 1-min.PNG (162.32 Kio) Vu 442 fois
-
- 2-min.PNG (46.73 Kio) Vu 442 fois
-
- 3-min (1).PNG (98.42 Kio) Vu 442 fois
Re: Intégrale de surface
Oui c'est bien ce que j'ai fait! (désolé les pièces jointes bugs==> elles ne s'affichent pas entièrement)
- Fichiers joints
-
- 4.PNG (90.62 Kio) Vu 431 fois
-
- 2-min.PNG (46.73 Kio) Vu 431 fois
-
- 3-min (1).PNG (98.42 Kio) Vu 431 fois
Re: Intégrale de surface
chan79 a écrit:
ensuite
par parties en posantet
etc
C'est faux non ??
int_{y=0}^x x*cos(x+y)dy=[x/y*sin(x+y)]_0^x ??
14 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 12 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
