trouver deux entiers naturels sachant quqe leur somme est 581 et que le quotient de leur PPCM par leur PGCD est 240.
En claire, a+b = 581 et PPCM(a,b)/PGCD(a,b)=240.
ET j'ai une espèce d'intuition comme quoi il faut utiliser le fait que : PPCM(a,b)*PGCD(a,b) = a*b mais je ne sais pas comment.
Exo PGCD PPCM
11 messages
- Page 1 sur 1
Ouais, pas facile !
Je pense qu'il est utile de considérer la décomposition en facteurs premiers de a et de b. Soient ,
, 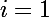 à
à 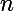 les n facteurs premiers intervenant dans la décomposition de a et b.
les n facteurs premiers intervenant dans la décomposition de a et b.
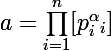 (certains des
(certains des 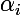 pouvant être nuls)
pouvant être nuls)
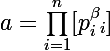 (certains des
(certains des  pouvant être nuls)
pouvant être nuls)
Soit D le PGCD de ces deux nombres, M, leur PPCM.
Alors :
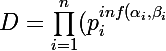}))
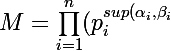}))
inf(x,y) désignant "le plus petit des deux nombres x et y)
sup(x,y) désignant "le plus grand des deux nombres x et y)
et
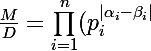)
Bon, je m'arrête ! Essaie de continuer !
Je pense qu'il est utile de considérer la décomposition en facteurs premiers de a et de b. Soient
Soit D le PGCD de ces deux nombres, M, leur PPCM.
Alors :
inf(x,y) désignant "le plus petit des deux nombres x et y)
sup(x,y) désignant "le plus grand des deux nombres x et y)
et
Bon, je m'arrête ! Essaie de continuer !
alben a écrit:Et si ! les données permettent d'obtenir (à un facteur d=pgcd près) la somme et le produit des deux nombres.
Il suffit d'écrire le delta de l'équation du second degré >0 pour obtenir une condition sur d et comme 581 n'a pas beaucoup de diviseurs...
Faut voir ! Je ne suis pas ennemi du colloque ! Lorsque lomdefer aura trouvé, nous comparerons nos solutions respectives !
(j'ai quand même trouvé la solution, au cas où tu en douterais !)
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 55 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
