Exo classique convexité

[dilzydils]

Bonjour

J'ai qq reminiscences à propos d'1 exo classique d'analyse dont j'aimerai que vous me donniez l'enonce si vous le connaissez.

C'est une inégalité f((x+y)/2)<(f(x)+f(y))/2..
Apres on parle de continuité, convexité et fonction affine...

Ca vous dit qq chose??

Merci

[tize]

Des exercices de ce genre il doit y en avoir un paquet...
peut être l'exo qui consiste à montrer que si f((x+y)/2)<=(f(x)+f(y))/2 et f est continue alors f est convexe mais si f n'est pas continue alors on peut f((x+y)/2)=(f(x)+f(y))/2 et f non continue...

[dilzydils]

Merci Tize

Pour montrer f convexe, il faut montrer que pour tout a dans [0;1], f(a*x+(1-a)*y)<=a*f(x)+(1-a)*f(y)..
On a la relation pour a=1/2, je ne vois pas comment utiliser la continuité de f pour montrer que c'est vrai pour tout a...
Help plz.

[tize]

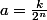
De mémoire (je sais plus trop...), on montre ceci par récurrence sur n avec tous les rationnels () ensuite on peut conclure avec la continuité de f et la densité des rationnels dans