Problème Mathématique
3 messages
- Page 1 sur 1
Problème Mathématique
J'ai un quadrillage régulier, j'enlève les lignes pour ne laisser que des points d'intersections. Mon quadrillage fait 10 points sur 10 points. Combien y a-t-il de carrés dont les sommets sont des points du quadrillage? Aidez-moi je n'y arrive pas avec les carrés qui sont en diagonale!!!
Re: Problème Mathématique
Salut,
Il y a des tonnes de façon de procéder plus ou moins longues et plus ou moins astucieuses.
Une méthode moyennement longue et moyennement astucieuse, c'est de regarder, pour chaque carré (en "biais" ou pas) quel est le plus petit carré à cotés parallèles au bord qui le contient.
Si ton grand carré de départ fait, en terme de longueurs, N-1 par N-1 (donc il y a N points sur chaque coté et N^2 points en tout), des carrés de longueur CxC dont les cotés sont parallèles aux bord, il y en a (N-C)^2 et dans chacun de ces carrés, on peut placer C carrés éventuellement "en biais" dont les sommets sont sur le bord du carré CxC.
Le nombre total de carrés est donc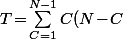^2\!=\!\cdots\!=\!\dfrac{N^2(N^2-1)}{12})
Vu le résultat (passablement simple), il doit sans doute y avoir une méthode plus astucieuse qui évite de passer par une somme.
Il y a des tonnes de façon de procéder plus ou moins longues et plus ou moins astucieuses.
Une méthode moyennement longue et moyennement astucieuse, c'est de regarder, pour chaque carré (en "biais" ou pas) quel est le plus petit carré à cotés parallèles au bord qui le contient.
Si ton grand carré de départ fait, en terme de longueurs, N-1 par N-1 (donc il y a N points sur chaque coté et N^2 points en tout), des carrés de longueur CxC dont les cotés sont parallèles aux bord, il y en a (N-C)^2 et dans chacun de ces carrés, on peut placer C carrés éventuellement "en biais" dont les sommets sont sur le bord du carré CxC.
Le nombre total de carrés est donc
Vu le résultat (passablement simple), il doit sans doute y avoir une méthode plus astucieuse qui évite de passer par une somme.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
3 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 52 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
