Devoir sur les exponentielle

[Frédericdu35]

Bonjour tout le monde voila je voudrais que quelqu'un m'aide pour mon devoir en Math sur les exponentielles car il me reste que cette partie a faire mais c'est justement cette partie que je comprend pas alors si quelqu'un serai gentil de pouvoir m'aider car ça fait depuis 2 jours que j'essaie mais sans succés et je me fais du mal pour rien :
Merci d'avance

On considère dans cette partie, que la fonction f est définie pour tout réel x par f(x) = e^x−0,5x²
On note Cf sa courbe représentative.
1. Résoudre dans R, l’équation f(x) = 1.

2. Un logiciel de calcul formel donne le résultat suivant :

Dériver exp ( x-x²/2)

(1−x)exp (x-x²/2)

a) Déterminer une équation de la tangente TA à la courbe Cf au point A d’abscisse 0.
b) Déterminer une équation de la tangente TB à la courbe Cf au point B d’abscisse 2.
3. On note f ′′ la fonction dérivée seconde de la fonction f .
a) Calculer f ′′(x).
b) Étudier la convexité de la fonction f .
c) La courbe Cf admet-elle des points d’inflexion ?
4. Tracer dans le repère fourni en annexe la courbe Cf représentative de la fonction f .
On placera les points d’abscisses 0, 1, 2 et on tracera les tangentes à la courbe en ces points.

[capitaine nuggets]

Salut !

Oui et alors qu'as-tu fait ? Où bloques-tu ?

[Frédericdu35]

je crois qu'il faut que je trace la courbe a la calculatrice et que je dois
conjecture la valeur de x et démontre que cette valeur vérifie f(x)=1
et puis pour les tangente je dois appliquer les formules :
y = f '(a) (x - a) + f(a) avec xA
et c'est la que je bloque car les exponentielle c'est la 1er fois que les Maths me pose problème

[capitaine nuggets]

Pour ma part, je ne vois pas où est le problème, tu connais la formule, il suffit juste de l'appliquer au point d'abscisse donné. Quel est le problème avec l'exponentielle ?

[Frédericdu35]

Je pense que c'est par rapport au exponentielle car j'ai jamais travailé sur ça car j'ai je viens juste d'avoir un nouveau prof de math, mais je vais essayer, je viens tien au courant du résultat

[Frédericdu35]

Je suis vraiment désolé mais je suis perdu car j'ai trouvé :
y = f '(a) (x - a) + f(a) avec xA
a=0 donc l'équation est de la forme : y = f'(a)(x-0)+f(0)
f(x)=0-0,5X0² = 0

[pascal16]

y = f '(a) (x - a) + f(a)
attention cette écriture différencie a : l'abscisse du point considéré et x, l'abscisse variable de l'équation de la droite tangente en (a;f(a)) à la courbe représentative de f.

Dériver exp ( x-x²/2) = (1−x)exp (x-x²/2)

pour a=0
f(0) = exp(0-0²/2)=1
f'(0)= (1−0)exp (0-0²/2)=1*1=1
la tangente en 0 a pour équation : y=1*(x-0)+1 soit y=x+1

[Frédericdu35]

Ok très bien donc je vais faire la même chose mais en replaçant le 0 par 2

[Frédericdu35]

J'ai trouvé :
a=2
Dériver exp (x-x²/2)=(1-x)exp(x-x²/2)
f(0)=exp(2-2²/2)=1
f'(0)=(1-2) exp(2-2²/2)=-1*1=-1
La tangente en 2 a pour équation : y = 1*x(-2)+(-1)

[pascal16]

j'avais pas mi la parenthèse au bon endroit, je corrige, et tu as inversé f et f' :

y = f '(a) (x - a) + f(a)

tangente en a=2
y = f '(2) (x - 2) + f(2)
y = -(x - 2) + 1

soit y= - x+3

[Frédericdu35]

Je suis vraiment désolé mais j'ai juste besoin de savoir comment calculer f''(x) car après le reste je sais faire. Merci d'avance

[capitaine nuggets]

Salut !

'y a pas de problème, si tu as des questions pose-les
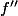. s'obtient en dérivée puisque par définition

[Frédericdu35]

d'accord pour ma part j'ai trouvé e^x, 5 x^2

[capitaine nuggets]

Je ne comprends pas ce que tu as voulu dire à partir de ce que tu as écris.

[Frédericdu35]

Bah j'ai essaier de dériver la fonction f mais je me suis trompé visiblement, je suis vraiment désolé du temps que je vous fait perdre

[capitaine nuggets]

Arrête, tu ne nous fait pas perdre du temps puisqu'on est là pour aider

pour ma part j'ai trouvé e^x, 5 x^2

Ca veut dire quoi ? f''(x)= e^x, 5 x^2 ? Quel sens à la virgule ?

[Frédericdu35]

Je pense que je me suis tout simplement trompé je pense que je dois dérivé f'(x)=(1−x)exp (x-(x²/2))
en utilisant cette formule comme dans mon cours mais je suis pas sur
(UV)'=U'V+UV'

[capitaine nuggets]

Oui, c'est ça.

[Frédericdu35]

Juste je voudrais savoir c'est quoi la dérivé de exp(x-x^2/2) car il me manque seulement ça s'il vous plait ?

[Frédericdu35]

A part si c'est f(x)=ex−0,5x2f(x)=ex−0,5x2
f′(x)=ex−0,5×2xf′(x)=ex−0,5×2x
f′(x)=ex−x
Mais je pense pas