Problème de proba

[Umbre373]

Bonjour,

Je cherche à exprimer en fonction de n la probabilité d'obtenir au moins un double (au moins deux 1, ou, au moins deux 2, ou, au moins deux 3, ou, au moins deux 4, ou, au moins deux 5, ou, au moins deux 6) en lançant n dés à six faces. Je trouve que c'est difficile car mes souvenirs de terms sont loin ! (je ne sais même plus si ce genre de proba étaient au programme)
Comme vous vous en doutez, c'est simplement pour un jeu de société donc pas d'urgence
Merci.

[pascal16]

C'est le genre de sujet de la seconde épreuve de CAPES (enfin, sa généralisation avec pfaces et n lancers).

pour se simplifier la vie, on peut commencer avec "faire 0 ou 1 fois 1 avec n dés", ça devient un dénombrement faisable.

[beagle]

euh je veux bien faire n = plus que 6 si vous voulez.

[pascal16]

au sens strict...

[beagle]

alors faut dire au moins un double donné

mais c'est dommage, au moins un double quelconque je me sentais en forme de le faire.

sinon c'est du binomial,
parce que si les n dés ne tiennent pas dans une petite main, on peut tout à fait les lancer un par un.
de même si on n'en a qu'un seul à la maison, on lancera n dés un par un pour y arriver.

[Umbre373]

Ok, si c'est trop difficile, pour un double quelconque ? Au début je me suis dit que c'était un calcul bateau, j'ai essayé et je bloque. Sur trois dés n = 3 , les deux premiers forment un double une fois sur 6, si ils sont différents (5 fois sur 6), le troisième a 2 chances sur 6 de former un double avec un des deux premiers. Après pour combiner ces cas là, puis passer à 4 dés, 5 dés ou plus, je ne sais pas faire.

[beagle]

donc c'est un double quelconque?
Ensuite tu veux un double mais si c'est un triple c'est pas bon,
Et comme c'est du quelconque tu acceptes deux doubles ou pas?
Je crois que je n'ai rien compris à ta demande en fait.

[Umbre373]

Oui, c'est un double quelconque, si c'est un triple j'accepte aussi (un triple contient bien un double), et oui s'il y a deux doubles ou plus , il y en a au moins un, donc c'est bon aussi.

[Ben314]

Salut,
Si on numérote les dés un "résultat", c'est une -uplet de chiffres entre 1 et 6 (compris).
Tout les -uplets sont équiprobable et il y en a .
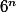
Reste à compter combien il y en a qui contiennent (au moins) un double.
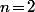
Pour 2 dés (), c'est facile, il y en a 6 donc une proba de de faire un double.
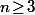
Pour , (mais évidement), c'est plus la m... et on a plutôt intérêt à compter les -uplets qui ne contiennent pas de double donc qui contiennent des chiffres tous différents. On doit d'abord choisir les chiffres parmi les 6 disponibles ce qui donne (coefficient binomial) puis multiplier par le nombre de façon de ranger les chiffres dans un certain ordre, c'est à dire . Au total, ça fait donc (ça s'appelle en fait un "arrangement", mais on s'en fout...)
Donc la proba de ne pas avoir de double est et la proba d'avoir un double est de
Pour , ca donne soit environ 16.67% ; 44.44% ; 72.22% ; 90.74% ; 98.46%.

P.S. C'est bien crado la façon dont MimeTeX met naturellement un 6^n au dénominateur (en tout cas chez moi...)

[Umbre373]

Ok ! Merci beaucoup ! C'est exactement ce que je voulais. J'ai mis un peu de temps à comprendre (j'ai dû aller chercher, pour me rappeler ce qu'était un coefficient binomial). C'est très astucieux de s'en servir pour compter les combinaisons où tous les dés donnent des résultats différents : toutes les autres combinaisons contiennent forcément au moins deux résultats identiques. Mais si je veux compter celles qui contiennent au moins un brelan ou un carré, je ne peux pas utiliser cette technique.

Bref, pour faire le cas général. Je sais que je suis gourmand mais comme j'aime bien les maths (et les jeux) : est-ce que quelqu'un sait quelle est la probabilité d'obtenir au moins k résultats identiques en lançant n fois un dé à p faces ? J'imagine que la formule doit être moche mais elle existe non ? Si je n'ai pas une belle explication comme pour le cas précédent, c'est pas grave, c'est certainement pas de mon niveau

[beagle]

tu pouvais faire comme tu avais commencé, mais avec l'astuce du 1 - pas de double.

pas de double, c'est comme tu faisais, sur n dés
premier dé 6/6
fois deuxième dé 5/6
fois troisième dé 4/6
...
bref c'est : 6 x 5x 4 x... / 6x6x6x...
tu as n éléments en haut , n éléments en bas

cette formule n'est pas belle à écrire d'où celle de ben314 qui dit la même chose avec une belle formule
mais souvent la méthode moche ci-dessus est plus facile à comprendre-retrouver.

(le résultat de chaque dé est indépendant des autres, lorsque l'on dit premier dé, deuxième dé, cela peut signifier tout plein de chose.Comme je l'avais dit on lance un seul dé n fois (parce que tu n'as que celui-là), et on peut examiner les dès dans l'ordre,ou dans n'importe quel ordre.Sinon pour rester sur un n lancer d'un seul coup, le premier dé est le premier dont je regarde le résultat, le deuxième dé est le deuxième dont je regarde le résultat...Bref tout ça c'est du pareil au même.)Au cas où quelq'un voudrait te demander c'est quoi le premier dé, en fait faufrait dire pour UN dé 6/6, alors UN deuxième dé est 5/6 pour pas doublon, UN troisième dé 4/6, etc...