Bonjour, pourriez-vous m'aider à cet exercice s'il vous plaît ?
Soit P(z)=z 3+(2−i)z 2+(2−2i)z−2i.
Le but de l'exercice est de trouver les racines de P.
1) P possède une racine imaginaire r 1. Calculer r 1.
Polynôme à coefficient complexe
4 messages
- Page 1 sur 1
Re: Polynôme à coefficient complexe
Salut !
On te dit que admet une racine imaginaire notée
admet une racine imaginaire notée 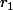 . Pose donc
. Pose donc 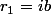 , avec
, avec  réel. Exprime alors
réel. Exprime alors ) sous forme algébrique. Tu auras alors que
sous forme algébrique. Tu auras alors que =0) si et seulement si
si et seulement si  ) = {\rm Im}(P(r_1))=0) .
.
= (ib)^3+(2-i)(ib)^2+(2-2i)(ib)-2i)
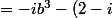b^2+(2-2i)(ib)-2i)
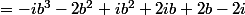
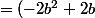 + i(- b^3+b^2+2b-2)) (arrivé ici, on peut remarquer qu'il est possible de factoriser les parties réelles et imaginaire).
(arrivé ici, on peut remarquer qu'il est possible de factoriser les parties réelles et imaginaire).
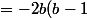 + i(- b^3+b^2+2b-2))
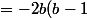 + i[ - (b-1)b^2+2(b-1)])
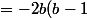 - i(b^2-2)(b-1)) (bien qu'on ait fini, je remarque que
(bien qu'on ait fini, je remarque que 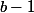 est un facteur commun donc je factorise par ce facteur ; ça va faciliter les choses).
est un facteur commun donc je factorise par ce facteur ; ça va faciliter les choses).
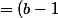[ -2b -i(b^2-2)])
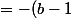[ 2b +i(b^2-2)])
=0) si et seulement si on a
si et seulement si on a 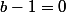 ou
ou  =0) (équation produit nul :
(équation produit nul : 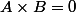 si et seulement si
si et seulement si 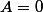 ou
ou 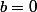 ). On a alors deux cas à distinguer :
). On a alors deux cas à distinguer :
- Si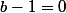 alors
alors 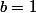 donc
donc  est une racine de
est une racine de  ;
;
- Si =0) alors en comparant les parties réelles et imaginaires comme annoncé plus haut, on a
alors en comparant les parties réelles et imaginaires comme annoncé plus haut, on a 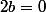 et
et 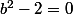 . Or si
. Or si 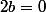 alors
alors 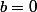 , mais
, mais  n'annule pas
n'annule pas 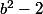 donc il n'existe pas de réel
donc il n'existe pas de réel  tel que l'on ait
tel que l'on ait  =0) .
.
En conséquence, ne peut valoir que
ne peut valoir que  et ainsi
et ainsi 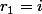 .
.

On te dit que
- Si
- Si
En conséquence,

- Merci de lire attentivement le règlement du forum.
- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.

- Comment écrire de belles formules mathématiques.
- Comment joindre une image ou un scan.
4 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 41 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
