Bonsoir,
pendant ma sieste, je me souvenu d'une phrase "C est algébriquement clos".
Je me suis dit, c'est vrai, mais ne va-t-on pas un peu vite dans la construction des ensembles.
Pour l'instant on dit que
N est créé par des axiomes (ppe, infinité, ordre total)
N devient Z par 'symétrisation', (Z,+) est un groupe
Z devient Q par recherche d'inverse par la loi * (Q,+,*) est un corps
et là on décide d'inclure les limites des suites de Q pour en faire R en disant que X²=2 n'a pas de solution dans Q.
puis i²=-1 nous apporte C.
mais attendez, on a sauté une étape
X²=2 n'a pas de solution dans Q, il faudrait donc d'abord trouver un ensemble qui contient Q et toutes les racines des polynômes de degré fini de Q. On sent les racine pièmes arriver et autres chiffres difficiles à écrire dont on ne connait qu'une approximation par développement décimal.
Pi n'est pas à ma connaissance, racine d'un polynôme à coefficient rationnel. Il y a donc un ensemble oublié au milieu de tout ça qui est loin d'être R.
Je me renseigne un peu, la clôture algébrique de Q existe... mais on ne sait pas la représenter ! On la note Q barre, clôture algébrique de Q (notation pas top car ce n'est pas l’adhérence de Q). Elle est dénombrable sous prétexte que c'est une union dénombrable de parties de Q. Ce qui veut dire au passage que les nombre réels qui ne sont pas racine de polynômes à coefficient rationnels (ou entiers relatif car c'est la même chose) sont ultra majoritaires dans R.
D'où ma question : est-ce que certains ont eut des résultats intéressants sur ce sujet, ou ont quelques mots ou noms qui me permettraient de trouver quelques résultats sympas sur la clôture algébrique de Q ?
Fermeture de Q
6 messages
- Page 1 sur 1
Re: Fermeture de Q
Je ne sais pas trop ce que tu entends par le fait qu'on ne sait pas "représenter" 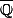 (il s'appelle le corps des nombres algébriques)... C'est quoi pour toi une "représentation" de
(il s'appelle le corps des nombres algébriques)... C'est quoi pour toi une "représentation" de  ou de
ou de  ? Ce qui est vrai c'est qu'a priori il n'est pas forcément simple de montrer qu'un complexe donné est algébrique ou pas (car il faut bien réaliser que dans
? Ce qui est vrai c'est qu'a priori il n'est pas forcément simple de montrer qu'un complexe donné est algébrique ou pas (car il faut bien réaliser que dans 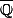 il y a des nombres complexes), mais après tout il n'est pas forcément simple de montrer qu'un réel donné est rationnel ou pas.
il y a des nombres complexes), mais après tout il n'est pas forcément simple de montrer qu'un réel donné est rationnel ou pas.
Le fait de vouloir donner des racines à tous les polynômes c'est justement le principe de la clôture algébrique. Il se trouve qu'en passant de à
à  on donne des racines à certains polynômes, mais ce n'est pas vraiment le but recherché. Le procédé qui permet de passer de
on donne des racines à certains polynômes, mais ce n'est pas vraiment le but recherché. Le procédé qui permet de passer de  à
à  s'appelle la complétion, et l'idée sous-jacente est de "boucher les trous" dans l'ensemble de départ en donnant des limites à toutes les suites de Cauchy.
s'appelle la complétion, et l'idée sous-jacente est de "boucher les trous" dans l'ensemble de départ en donnant des limites à toutes les suites de Cauchy.
Pour caricaturer un peu, la clôture algébrique c'est un truc d'algébriste (ça parle de polynômes et de racines), la complétion c'est un truc d'analyste (ça parle de métrique et de limites). Le must étant bien sûr d'avoir un espace à la fois complet et algébriquement clos. Comme n'est ni l'un ni l'autre, soit tu complètes d'abord puis tu clos (ça donne
n'est ni l'un ni l'autre, soit tu complètes d'abord puis tu clos (ça donne  puis
puis  ), soit tu clos d'abord puis tu complètes (ça donne
), soit tu clos d'abord puis tu complètes (ça donne 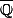 puis
puis  ).
).
En cherchant "nombres algébriques" sur le net tu devrais pouvoir trouver suffisamment d'infos et de détails.
Le fait de vouloir donner des racines à tous les polynômes c'est justement le principe de la clôture algébrique. Il se trouve qu'en passant de
Pour caricaturer un peu, la clôture algébrique c'est un truc d'algébriste (ça parle de polynômes et de racines), la complétion c'est un truc d'analyste (ça parle de métrique et de limites). Le must étant bien sûr d'avoir un espace à la fois complet et algébriquement clos. Comme
En cherchant "nombres algébriques" sur le net tu devrais pouvoir trouver suffisamment d'infos et de détails.
Re: Fermeture de Q
Merci pour ta réponse.
Dans la construction mathématique des ensembles donnée aux élèves, l'exemple cité partout est que n'est pas rationnel ou que x²=2 n'a pas de solution dans Q .
n'est pas rationnel ou que x²=2 n'a pas de solution dans Q .
On le cite car on a une démonstration (très académique et obligatoire) à placer mais ce qu'on fait ensuite est un peu différent.
On va ensuite sur résolution par dichotomie, on construit deux suites adjacentes et on passe à la limite. On construit alors R comme "toutes le limites possibles d'une suite d'éléments de Q".
Le chemin proposé, la recherche d'une racine d'un polynôme, ne donne pas vraiment R, mais la partie réelle des nombres algébriques. C'est là que je trouve bizarre qu'en prépa on ait pas 2 minutes de cours sur ce qui me semble être un corps défini implicitement et qui pourrait donner des exo sur les polynômes sympa.
Si a est une racine non nulle d'un polynôme à coefficients entiers-ou-rationnels, est-ce que 1/a est aussi racine d'un autre polynôme ?
Etant donné un nombre réel, comment trouver un polynôme dont il est racine. Le cas échéant quels sont les critères pour que ce nombre réel ne soit pas racine d'un polynôme (ça sent la construction de suite qui doivent être nulles à partir d'un certain rang) ? (c'est à ce que j'ai compris ce qu'on ne sait pas faire, ie, on ne sait pas a priori si un nombre réel est dans Qbarre)
Dans la construction mathématique des ensembles donnée aux élèves, l'exemple cité partout est que
On le cite car on a une démonstration (très académique et obligatoire) à placer mais ce qu'on fait ensuite est un peu différent.
On va ensuite sur résolution par dichotomie, on construit deux suites adjacentes et on passe à la limite. On construit alors R comme "toutes le limites possibles d'une suite d'éléments de Q".
Le chemin proposé, la recherche d'une racine d'un polynôme, ne donne pas vraiment R, mais la partie réelle des nombres algébriques. C'est là que je trouve bizarre qu'en prépa on ait pas 2 minutes de cours sur ce qui me semble être un corps défini implicitement et qui pourrait donner des exo sur les polynômes sympa.
Si a est une racine non nulle d'un polynôme à coefficients entiers-ou-rationnels, est-ce que 1/a est aussi racine d'un autre polynôme ?
Etant donné un nombre réel, comment trouver un polynôme dont il est racine. Le cas échéant quels sont les critères pour que ce nombre réel ne soit pas racine d'un polynôme (ça sent la construction de suite qui doivent être nulles à partir d'un certain rang) ? (c'est à ce que j'ai compris ce qu'on ne sait pas faire, ie, on ne sait pas a priori si un nombre réel est dans Qbarre)
Re: Fermeture de Q
Réponse : oui et là, c'est complètement évident. (et que les coeff. du polynôme soit entiers ou rationnels ne change rien : s'il sont rationnels, en multiplianty le polynôme par le ppcm des dénominateur, on se ramène à des coeff entiers).pascal16 a écrit:Si a est une racine non nulle d'un polynôme à coefficients entiers-ou-rationnels, est-ce que 1/a est aussi racine d'un autre polynôme à coefficients entiers?
Là où c'est nettement plus "chaud", c'est de montrer que si a et b sot racines de P et Q respectivement (à coeff entiers) alors a+b est lui même racine d'un polynôme à coeff. entier.
Et encore plus chaud, c'est de montrer que si on a un polynôme dont les coefficients sont racines de polynômes à coeff. entiers alors les racines de ce polynômes sont aussi racines de polynômes à coeff. entiers (i.e que quans on "ajoute" les racines des polynômes à coeff entiers, c'est pas la peine de le refaire ensuite...)
Tout dépend de la "forme" sous lauelle on te donne le polynôme. Si on le le donne sous la forme d'une expression avec des racines n-ièmes (éventuellement emboités), c'est pas trop difficile. Si on te le donne sous une autre forme, ça peut être plus coton.pascal16 a écrit:Etant donné un nombre réel, comment trouver un polynôme dont il est racine.
Pour montrer qu'un nombre n'est pas algébrique, on procède (évidement) par l'absurde. Cherche la preuve du fait que e (la base de l'exponentielle) est transcendant (= non algébrique) : c'est pas "super dur" (mais c'est très astucieux) et ça te donnera des idées concernant le "comment on procède en général".pascal16 a écrit:Le cas échéant quels sont les critères pour que ce nombre réel ne soit pas racine d'un polynôme (ça sent la construction de suite qui doivent être nulles à partir d'un certain rang) ? (c'est à ce que j'ai compris ce qu'on ne sait pas faire, ie, on ne sait pas a priori si un nombre réel est dans Qbarre)
Et il n'y a bien entendu pas de "méthode générale" en particulier du fait que tout dépend de la façon dont on te "donne" le réel de départ (celui dont tu doit dire s'il est ou s'il n'est pas algébrique).
Modifié en dernier par Ben314 le 25 Oct 2017, 13:32, modifié 1 fois.
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Fermeture de Q
Merci beaucoup.
Je sais que je ne trouverais pas de réponse parfaite, mais je suis sur de trouver quelques constructions de polynômes sympas.
@+
Je sais que je ne trouverais pas de réponse parfaite, mais je suis sur de trouver quelques constructions de polynômes sympas.
@+
Re: Fermeture de Q
pascal16 a écrit:Merci pour ta réponse.
Dans la construction mathématique des ensembles donnée aux élèves, l'exemple cité partout est quen'est pas rationnel ou que x²=2 n'a pas de solution dans Q .
On le cite car on a une démonstration (très académique et obligatoire) à placer mais ce qu'on fait ensuite est un peu différent.
Oui quand on introduit les grands ensembles de nombres, c'est souvent illustré par des équations qui "gagnent" des solutions à chaque étape. Mais s'en servir de justification genre "on a vu plus grand parce qu'on voulait donner des solutions à telle équation" est fumeux et parachuté. Ne serait-ce que parce que c'est faux historiquement, et qu'au niveau scolaire où on rencontre les grands ensembles de nombres pour la première fois, la "définition" (qui n'en est pas une) qu'on donne de
En revanche ce qui peut être intéressant c'est d'essayer de faire sentir pourquoi on peut avoir envie de donner des solutions à certaines équations en particulier.
6 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 23 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
