Intégrale

[GrosLapin]

Salut à tous,

Je bloque sur cette égalité depuis un moment maintenant...
Quelqu'un peut m'expliquer comment passe t on à la 2eme ligne?

Merci d'avance

[Lostounet]

Salut GrosLapin xD..

C'est simple: la fonction sous l'intégrale est de la forme u'/u.
U(x)=x^2-4x+8
U'=2x-4

Donc ceci n'est que la dérivée de ln(U)

[GrosLapin]

Excellent, merci à toi!

[Black Jack]

Salut,

Attention quand même à la signification des signes "=" dans ce genre de manipulation.

On aurait tout aussi bien pu remplacer la 2ème ligne par 3/2.ln(x²-4x+8) + 17 (par exemple)

Mais on ne peut quand même pas dire que 3/2.ln(x²-4x+8) est égal à 3/2.ln(x²-4x+8) + 17

Une primitive est définie à une constante près ... et donc méfiance à l'interprétation des signes "="

Et encore, ici, on a de la "chance" car x²-4x+8 > 0 pour tout x.

Si dans le sujet, on remplaçait (par exemple) le 8 du dénominateur par un 1, sauf indication spécifique sur les valeurs possibles pour x, on devrait remplacer les ( ) de la 2ème ligne par des valeurs absolues... et le problème de la constante d'intégration serait encore présent.

Ma réponse est peut-être en "overdesign" avec ce qui est attendu.

[pascal16]

Tout à fait BlackJack, ces approximations n'ont plus place dans le supérieur.

[Lostounet]

Mouais.. mais bon si tu veux faire dans la rigueur déjà avant la constante d'intégration ....le signe intégrale sans bornes c'est moyen.

Pour moi quand il y a un signe intégrale avec deux bornes, il n' y a pas de constante d'intégration vu qu'elles se simplifient. Et si tu veux mettre une intégrale sans borne à la physicienne... ben on fait ce qu'on veut avec la constante c. :p

C'est pas comme si on était rigoureux :p on ne donne même pas le domaine de définition de ces primitives/dérivées!

[pascal16]

la valeur absolue dans le ln doit être un réflexe

[aviateur]

Bonjour
Je ne sais pas si il y a une règle bien définie pour le symbole intégral (sans les bornes).
Moralement, tout au moins pour moi, cela veut dire "une primitive de f(x) est égale à".
De ce point de vue je suis en accord avec la réponse de @Lostounet.
Evidemment cela pose des problèmes du point de vue rigueur avec le symbole "égalité", mais seulement pour celui qui veut bien.
Maintenant le seul soucis est du point de vue pédagogique. Là, de préférence, il vaut mieux faire attention à l'élève qui ne possède pas le recul et voir comment on explique cette notion au lycée.

Ceci étant dit, par sécurité, il est préférable de regarder avant tout sur quel(s) intervalle(s) on travaille.

[Lostounet]

mais seulement pour celui qui veut bien.

Les physiciens appliqués ont cette fâcheuse habitude de te poser un sujet avec 70 approximations dans l'énoncé.

Et pour corriger ta copie ils t'enlèvent les 3/4 des points si tu ne mets pas des +c pour "manque de rigueur". Ou si tu divises par théta ("attention l'angle peut théoriquement s'annuler")

[Ben314]

Salut,
Les gouts et les couleurs, c'est chacun les siens, mais perso., je n'ai jamais utilisé ce type de notation, ni pour moi, ni avec mes étudiants du fait que je trouve que c'est un vrai piège à c...
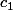
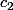
Par exemple, si on te demande quelle sont les primitives de alors la VRAIE réponse, c'est les fonction de la forme où les constantes et n'ont aucune raison d'être les mêmes.
Et si tu écrit bien proprement que les primitives on les trouves en calculant tu est sensé immédiatement voir que, dans un cas pareil, si tu choisi un xo>0, tu ne pourra prendre que des x>0 et réciproquement.
Et c'est pas gagné non plus avec ce type de notation de calculer des primitive en faisant un changement de variable dans l'intégrale vu que comme il y a pas de bornes, on ne garde pas "la trace" du changement de variable dans l'expression que l'on écrit.
Bref, pour le peu que ça gagne (deux symboles qu'on écrit pas), a mon sens, ça vaut franchement pas le coup.