Bonjour,
j'ai une question à poser sur les foyers des coniques.
Une conique est donnée par un foyer F une excentricité e et une directrice D. À priori il n'y a aucune raison pour que, pour e donnée, le couple (F,D) soit le seul à engendrer une certaine conique. En effet les hyperboles et les ellipses admettent deux foyers avec leurs directrices associées.
Les questions que j'ai sont:
1) Pourquoi les paraboles n'admettent qu'un couple (F,D) générateur pour e donnée.
2) Pourquoi les ellipses et les hyperboles n'en admettent pas plus de deux.
Je n'ai pas trouvé les réponses à ça sur le net....
[MPSI] Question de cours coniques
8 messages
- Page 1 sur 1
JBB a écrit:snif...personne n'aime mes coniques...
Si, si ! J'aime bien !
Mais tu poses des questions...bizarres ! Je n'ai pas vraiment de réponse.
Les coniques, ce sont des intersections de cônes avec un plan. S'il s'agit d'un cône "de révolution", dans le cas des ellipses, le plan en question coupe une nappe selon une courbe fermée (tiens, pourquoi n'as tu pas posé la question "les hyperboles et les paraboles sont des courbes avec des points à l'infini, pas les ellipses ! Pourquoi ?"). Pour démontrer une propriété sur la somme des distances des points de l'ellipse à deux points particuliers appelés foyers, on est amené à considérer une sphère qui serait tangente à la fois à une nappe à l'intérieur de celle-ci, et au plan. Il se trouve qu'il y en a deux, et les foyers sont les poitns de tangence au plan. Dans le cas de l'hyperbole, le plan coupe les deux nappes, et on trouve encore deux sphères (une dans chaque nappe) qui soit tangente à la nappe et tangente au plan. Les deux points de tangence des sphères avec le plan ont des propriétés très particulières : on les appellent aussi foyers. Il y en a deux. Dans le cas de la parabole, le plan ne coupe qu'une seule nappe car il est parallèle à une directrice. Si on cherche des sphères tangentes à l'une des nappes et au plan, on n'en trouve qu'une seule ! Le point de tangence a lui aussi de très intéressantes propriétés géométriques et on lui a donc donné un nom : le foyer. Il n'y en a qu'un ! Pourquoi ! Va savoir... :ptdr: Je n'ai pas d'explication !
Je confirme que tes questions sont strange.
Il va de soi qu'une parabole possède un unique foyer et une unique directrice. Il existe des tas de caractérisations géométriques de ces deux objets qui montrent leur unicité. Je te livre les deux premières qui me viennent à l'esprit :
- Le foyer est le point de concours des rayons lumineux parallèles à l'axe et réfléchis par la parabole.
- La directrice est le lieu des points d'où l'on voit la parabole sous un angle droit.
C'est un peu comme si tu demandais pourquoi un cercle possède un seul centre.
Il va de soi qu'une parabole possède un unique foyer et une unique directrice. Il existe des tas de caractérisations géométriques de ces deux objets qui montrent leur unicité. Je te livre les deux premières qui me viennent à l'esprit :
- Le foyer est le point de concours des rayons lumineux parallèles à l'axe et réfléchis par la parabole.
- La directrice est le lieu des points d'où l'on voit la parabole sous un angle droit.
C'est un peu comme si tu demandais pourquoi un cercle possède un seul centre.
Merci à tous les deux, en fait le problème que j'ai eu c'est que la définition monofocale des coniques n'implique rien sur le nombre de foyers qu'une conique admet. Avec les définitions de foyers que vous proposez il est possible de déterminer le nombre de foyers d'une conique.
Mais à partir de la définition:
une conique d'excentricité e, foyer F et directrice associée D est l'ensemble tq d(F,M)=ed(M,D) je n'ai pas réussi à prouver quoi que ce soit sur le nombre maximal de foyers d'une conique donnée. J'admets que c'est étrange, mais en toute rigueur la définition monofocale ne précise rien là dessus.
En effet, avec la définition euclidienne les sphères tangentes aux nappes et au plan permettent de dénombrer les foyers.
Et quitte à m'exposer à une certaine maniaquerie, rien ne garantit qu'un cercle possède un seul centre (merci beaucoup cet exemple me sert vraiment!)
Définition: C(O,R) ={M tq d(O,M)=R)} mais rien ne garantit qu'il n'existe pas d'autre couple (O',R') tq un ensemble du type {M tq d(O',M)=R'} ne coincide pas qvec le précédent.
Je suis sûr que je fqis une grosse bourde de raisonnement, mais pour être sincère je ne la vois pas....
Modification: j'ai réfléchi sur le sujet avec un ami si désastreux que moi en maths et nous avons bonnement conclu que rien ne prouve qu'un cercle admet un seul couple (centre, rayon) mais qu'on s'en fiche car on en a assez de savoir qu'il en qdmet un. Dans toutes les démos que nous avons vues on n'utilise jamais l'unicité de (O, R) tout au plus l'unicité d'un élément du couple ayant fixé l'autre. Voilà, seulement pour vous faire rigoler avec mes prises de tête et encore merci de vos réponses!
Mais à partir de la définition:
une conique d'excentricité e, foyer F et directrice associée D est l'ensemble tq d(F,M)=ed(M,D) je n'ai pas réussi à prouver quoi que ce soit sur le nombre maximal de foyers d'une conique donnée. J'admets que c'est étrange, mais en toute rigueur la définition monofocale ne précise rien là dessus.
En effet, avec la définition euclidienne les sphères tangentes aux nappes et au plan permettent de dénombrer les foyers.
Et quitte à m'exposer à une certaine maniaquerie, rien ne garantit qu'un cercle possède un seul centre (merci beaucoup cet exemple me sert vraiment!)
Définition: C(O,R) ={M tq d(O,M)=R)} mais rien ne garantit qu'il n'existe pas d'autre couple (O',R') tq un ensemble du type {M tq d(O',M)=R'} ne coincide pas qvec le précédent.
Je suis sûr que je fqis une grosse bourde de raisonnement, mais pour être sincère je ne la vois pas....
Modification: j'ai réfléchi sur le sujet avec un ami si désastreux que moi en maths et nous avons bonnement conclu que rien ne prouve qu'un cercle admet un seul couple (centre, rayon) mais qu'on s'en fiche car on en a assez de savoir qu'il en qdmet un. Dans toutes les démos que nous avons vues on n'utilise jamais l'unicité de (O, R) tout au plus l'unicité d'un élément du couple ayant fixé l'autre. Voilà, seulement pour vous faire rigoler avec mes prises de tête et encore merci de vos réponses!
JBB a écrit:Et quitte à m'exposer à une certaine maniaquerie, rien ne garantit qu'un cercle possède un seul centre (merci beaucoup cet exemple me sert vraiment!)
Définition: C(O,R) ={M tq d(O,M)=R)} mais rien ne garantit qu'il n'existe pas d'autre couple (O',R') tq un ensemble du type {M tq d(O',M)=R'} ne coincide pas qvec le précédent.
Je suis sûr que je fqis une grosse bourde de raisonnement, mais pour être sincère je ne la vois pas....
Modification: j'ai réfléchi sur le sujet avec un ami si désastreux que moi en maths et nous avons bonnement conclu que rien ne prouve qu'un cercle admet un seul couple (centre, rayon) mais qu'on s'en fiche car on en a assez de savoir qu'il en qdmet un. Dans toutes les démos que nous avons vues on n'utilise jamais l'unicité de (O, R) tout au plus l'unicité d'un élément du couple ayant fixé l'autre. Voilà, seulement pour vous faire rigoler avec mes prises de tête et encore merci de vos réponses!
Le cas est plus grave que je ne pensais. Non je plaisante. Tu as le mérite de poser des questions que certains n'oseraient pas poser, ou ne verraient même pas.
Pour le cas du cercle, il me semble que c'est facile tout de même. Il te suffit de caractériser O et R géométriquement d'une façon ou d'une autre.
Par exemple O est centre de symétrie et s'il y avait deux centres de symétrie, le cercle serait invariant par une translation de vecteur non nul (la composée des deux symétries) et donc serait une partie non bornée du plan...
R est le demi-diamètre et le diamètre d'une partie compacte du plan est parfaitement défini.
On peut trouver des tas d'autres caractérisations de ce type. Et on n'utilise rien d'autre que la définition du cercle que tu as donnée.
Qu'en pensent les autres?
JBB, tes questions sont réellement importantes, et
ces problèmes sont généralement bien maltraités dans les manuels.
Il est effectivement impossible de résoudre ce problème de manière immédiate à partir de la définition. Pour trouver les couples foyers-directrice possibles,
on peut utiliser les similitudes :
si on a deux couples foyers directrice (F,D) et (F',D')
définissant E pour l'excentricité e, alors il existe une similitude directe s envoyant F sur F' et D sur D', et donc s(E)=E.
Par exemple pour l'ellipse E d'équation réduire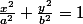
dans un certain repère orthonormal d'origine O, on prouve d'abord que O
est le seul centre de symétrie de E. La similitude s doit donc fixer O,
puis préserver globalement la paire constituée des points de coordonnées respectives (a,0) et (-a,0), car ce sont les points de E à distance maximale
de O. On en déduit que s est l'identité ou la symétrie de centre O.
Il s'ensuit qu'il existe au plus deux couples foyer-directrice associés à E
pour l'excentricité e.
Pour le cas du cercle, le rayon R se retrouve comme moitié de la distance
maximale entre deux points du cercle. Une fois le rayon trouvé,
le centre s'obtient comme milieu de n'importe quel segment quelconque formé sur le cercle et dont la longueur vaut 2R.
ces problèmes sont généralement bien maltraités dans les manuels.
JBB a écrit:Mais à partir de la définition:
une conique d'excentricité e, foyer F et directrice associée D est l'ensemble tq d(F,M)=ed(M,D) je n'ai pas réussi à prouver quoi que ce soit sur le nombre maximal de foyers d'une conique donnée.
Il est effectivement impossible de résoudre ce problème de manière immédiate à partir de la définition. Pour trouver les couples foyers-directrice possibles,
on peut utiliser les similitudes :
si on a deux couples foyers directrice (F,D) et (F',D')
définissant E pour l'excentricité e, alors il existe une similitude directe s envoyant F sur F' et D sur D', et donc s(E)=E.
Par exemple pour l'ellipse E d'équation réduire
dans un certain repère orthonormal d'origine O, on prouve d'abord que O
est le seul centre de symétrie de E. La similitude s doit donc fixer O,
puis préserver globalement la paire constituée des points de coordonnées respectives (a,0) et (-a,0), car ce sont les points de E à distance maximale
de O. On en déduit que s est l'identité ou la symétrie de centre O.
Il s'ensuit qu'il existe au plus deux couples foyer-directrice associés à E
pour l'excentricité e.
Pour le cas du cercle, le rayon R se retrouve comme moitié de la distance
maximale entre deux points du cercle. Une fois le rayon trouvé,
le centre s'obtient comme milieu de n'importe quel segment quelconque formé sur le cercle et dont la longueur vaut 2R.
Par exemple O est centre de symétrie et s'il y avait deux centres de symétrie, le cercle serait invariant par une translation de vecteur non nul (la composée des deux symétries) et donc serait une partie non bornée du plan...
C'est joli ça...j'y aurais jamais pensé! Et j'aurais encore moins pensé à utiliser des similitudes...
Merci à tous je vais recopier vos démos dans mes cours!
8 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 35 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
