bonjour
Exercice de 1 ere sur le second degre
Il faut resoudre 9/x - x/3 =3
No problemo. On arrive à
x^2 +9x -27=0 avec 2 racines: 2,27 et -11,37 le tout pour x<> 0
par curiosité, j ai tracé la courbe de la premiere expression, puis de la deuxieme. Et je me trouve avec deux courbes distinctes. Ok, elles coupent les x aux mêmes endroits et il y a une asymptote ( je crois que c'est le bon mot) pour x=0.
Pourtant, les deux equations sont equivalentes non?
Merci!
Deux equations equivalentes mais...
11 messages
- Page 1 sur 1
Re: deux equations equivalentes mais...
ifebo a écrit:Pourtant, les deux equations sont equivalentes non?
Merci!
salut
Ce ne sont pas les mêmes fonctions (elles n'ont même pas le même ensemble de définition). Leurs courbes représentatives sont différentes. Mais elles s'annulent pour les mêmes valeurs:
g est le produit de f par la fonction x ---> -3x
Re: deux equations equivalentes mais...
Merci pour la reponse
Pour resoudre la 1), je reduis au même dénominateur (ce qui, a priori, ne devrait rien changer), et j obtiens la 2).
Ce serait cette operation qui fait que 1) est different de 2)? Ben j aurais pas cru!
Pour resoudre la 1), je reduis au même dénominateur (ce qui, a priori, ne devrait rien changer), et j obtiens la 2).
Ce serait cette operation qui fait que 1) est different de 2)? Ben j aurais pas cru!
Re: deux equations equivalentes mais...
En réduisant au même dénominateur, tu multiplies par -3x. Tu modifies la fonction mais tu ne changes pas les racines.
De même, si tu as à résoudre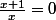
Cette équation a les mêmes solutions que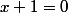
Les courbes sont différentes.
De même, si tu as à résoudre
Cette équation a les mêmes solutions que
Les courbes sont différentes.
Re: deux equations equivalentes mais...
Pourtant, les deux equations sont equivalentes non?
C'est le bon vocabulaire que tu emploies, les équations sont équivalentes, c'est à dire qu'elles ont les mêmes solutions... peut importe le chemin qui y mène.
Re: deux equations equivalentes mais...
Merci....
Sans vouloir chipoter, si les deux equations sont equivalentes, il en existe alors une infinité, qui auront toutes les mêmes racines, mais chacune aura sa représentation graphique propre à elle...C est ça?
Sans vouloir chipoter, si les deux equations sont equivalentes, il en existe alors une infinité, qui auront toutes les mêmes racines, mais chacune aura sa représentation graphique propre à elle...C est ça?
Re: deux equations equivalentes mais...
l'équation x = 1 est équivalente à l'équation 2x = 2 qui est équivalente à l'équation 3x = 3 qui est équivalente à ....
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: deux equations equivalentes mais...
Tu mélanges un peu les notions d'équations et de représentations graphiques de fonctions.
Je prends un autre exemple:
Equation A:
(x-1)(x-2)=0
Equation B:
(x-1)(x-2)(x²+1)=0
Si l'une des égalités est vraie, l'autre aussi. Elles sont équivalentes.
Maintenant, si on considère les fonctions f et g:
f(x)=(x-1)(x-2)
g(x)=(x-1)(x-2)(x²+1)
f et g s'annulent pour les mêmes valeurs.
Elles n'ont pas la même représentation graphique.
Je prends un autre exemple:
Equation A:
(x-1)(x-2)=0
Equation B:
(x-1)(x-2)(x²+1)=0
Si l'une des égalités est vraie, l'autre aussi. Elles sont équivalentes.
Maintenant, si on considère les fonctions f et g:
f(x)=(x-1)(x-2)
g(x)=(x-1)(x-2)(x²+1)
f et g s'annulent pour les mêmes valeurs.
Elles n'ont pas la même représentation graphique.
- Fichiers joints
-
- Image1.gif (12.04 Kio) Vu 451 fois
Re: deux equations equivalentes mais...
chan79 a écrit:f et g s'annulent pour les mêmes valeurs.
Elles n'ont pas la même représentation graphique.
C'est précisemment ce que je dis dans mon dernier post!
j ai aussi compris, merci zygomatique, que deux equations equivalentes peuvent avoir la même rep. graph. Mais c est pas une fatalité.
Merci!
Re: deux equations equivalentes mais...
ifebo a écrit:Merci....
Sans vouloir chipoter, si les deux equations sont equivalentes, il en existe alors une infinité, qui auront toutes les mêmes racines, mais chacune aura sa représentation graphique propre à elle...C est ça?
C'est toute la beauté de la chose...
Une équation donnée est équivalente à une infinité d'autres équations: tu peux multiplier par une constante non nulle, ajouter x^2 aux deux membres.
Les fonctions en jeu deviennent alors très différentes mais la solution est conservée! Le jeu est de trouver une série d'équivalences qui amène vers une forme plus simple de l'équation pour la résoudre.
Merci de ne pas m'envoyer de messages privés pour répondre à des questions mathématiques ou pour supprimer votre compte.
11 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 64 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
