Problème de Somme
33 messages
- Page 2 sur 2 - 1, 2
Re: Problème de Somme
HagerFall a écrit:
C'est faux écrit comme sa même si je sais que c'est juste que tu la mal écrit en latex.
Mais pour être sur la bonne formule c'est sa :
Donc qui vaut
Re: Problème de Somme
HagerFall a écrit:Et du coup pour la suite je dois utiliser la même démarche ?
Par contre pour le calcul de cette somme sa sera encore plus dur et plus long que la précédente car t'aura un k² devant ton coefficient binomial cette fois ci et donc il te faudra utiliser la ruse suivante :
k²=k+k(k-1)
Et tu pourra réussir normalement avec cette indication
PS: N'oublie pas que les termes qui ne dépende pas de l'indice de la somme (ici k) on peut les faire sortir de la somme !!!!!!
Re: Problème de Somme
HagerFall a écrit:Ok merci encore je continuerais ça demain
Oui tu as raison, les calculs comme sa c'est fatiguant
J'espère que ton DM ce n'est pas que des questions de ce type.
Re: Problème de Somme
Salut,
Si ça t'interesse, en fait, il y a (au moins) deux façon de "virer" les k(k-1) qui te font c... dans la formule :
-Soit tu fait comme le dit Infernaleur en les "rentrant" dans les coeff. binomiaux pour faire "sortir" des n à la place (que tu va pouvoir sortir de la somme vu que ça ne dépend plus de k)
- Soit tu dit qu'ils proviennent d'une dérivation :
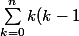{n \choose k}x^k(1-x)^{n-k}<br />=(1-x)^n\sum_{k=0}^{n}k(k-1){n \choose k}\Big(\dfrac{x}{1-x}\Big)^k)
^n\Big(\dfrac{x}{1-x}\Big)^2\sum_{k=0}^{n}k(k-1){n \choose k}\Big(\dfrac{x}{1-x}\Big)^{k-2})
(pour différent de 0 et de 1)
différent de 0 et de 1)
Or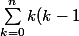{n \choose k}y^{k-2}) c'est la dérivée seconde (en
c'est la dérivée seconde (en  ) de
) de ^n) donc ça vaut
donc ça vaut (1+y)^{n-2}) .
.
Si ça t'interesse, en fait, il y a (au moins) deux façon de "virer" les k(k-1) qui te font c... dans la formule :
-Soit tu fait comme le dit Infernaleur en les "rentrant" dans les coeff. binomiaux pour faire "sortir" des n à la place (que tu va pouvoir sortir de la somme vu que ça ne dépend plus de k)
- Soit tu dit qu'ils proviennent d'une dérivation :
(pour
Or
Qui n'entend qu'un son n'entend qu'une sonnerie. Signé : Sonfucius
Re: Problème de Somme
Ah oui elle est pas mal cette méthode, bien joué
(surtout si on avait pas ce x/1-x qui complique les calculs)
(surtout si on avait pas ce x/1-x qui complique les calculs)
33 messages
- Page 2 sur 2 - 1, 2
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 39 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :
