Endomorphisme de polynômes

[unutilisateur]

Bonjour,
J'ai un petit problème pour répondre à une question, et j'aimerais votre aide..
M'est donné une application
J'ai déterminé le noyau de et Ker( )=, et le degré de en fonction de : deg( deg(
La quesiton qui m'est posée est la suivante : montrer que et et comparer les degrés de P et Q
J'ai commencé une analyse synthèse :
Soit tq et
Par évaluation en 0
et deg() deg()
càd par hypothèse deg(P) deg()
Et après je bloque....
Pourriez vous m'orienter
Merci d'avance
Bonne fin d'après midi

[pascal16]

essais avec p(X)= aX²+bX+c
calcule p(X+1)-P(X)
si tu regardes comment ça se passe :
-> les termes de plus haut degrés s'en vont.
-> le second reste, c'est en fait le degré de P (par la formule du binôme de Newton dans le cas général)
donc pour n>=2, deg(delta(P))=deg(P)-1
tu peux rajouter le cas deg(P)=1 et traiter à part le cas deg(P)=0

Donc si Q existe, on a deg(Q)=deg(P)+1
monter que Q existe, je rame un peu aussi, j'ai pas regardé si la récurrence était facile où s'il fallait faire plus directe.

[Ben314]

Salut,
Histoire de raisonner avec des e.v. de dimension fini (toujours plus pratique...), il peut être intéressant de fixer un entier et de considérer la restriction de ton endomorphisme (ce qui est cohérent vu que tu as déjà montré que si P est non constant)
Maintenant qu'on est en dimension fini, quelle est la dimension de ?
Qu'est ce qu'on en déduit concernant la dimension de ? ça signifie quoi ?
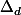
Enfin, que peut-on dire de l'ensemble des antécédents par d'un polynôme ? (sans chercher à expliciter cet ensemble, juste décrire de quel "type" il est...)

P.S. Concernant le degré de , ça serait mieux d'avoir une vraie égalité et pas une simple majortion comme tu l'a écrit (c'est d'ailleurs ce que pascal écrit dans son précédent post. et la formule qu'il donne est même valable pour d°(P)=1 : y'a que dans le cas d°(P)=0 que ça déconne, mais c'est normal vu que 0-1=-1 et qu'il n'y a pas de polynômes de degré -1)