Inéquation

[FLBP]

Bonjour,

Voilà un petit problème sympa :
- Vérifier sans calculatrice que cette inéquation est correcte :



Cordialement.

[zygomatique]

salut






ha merde ça ne marche pas !!!

[FLBP]

Dommage, c'était bien essayé.
Sinon moi, j'arrive à quelque chose du style :

[Lostounet]

Hello
Notons S le membre de gauche.
Le produit P des 4 membres de gauche vaut
ln(6)/ln(2) = 1 + ln(3)/ln(2) > 1 + 3/2 = 2.5
(Car 2ln(3) > 3 ln(2) car ln(9)>ln(8))

En appliquant l'inégalité arithmético-géométrique:
P^(1/4) < S/4

P^(1/4) > 2.5^(1/4) > (225)/100^(1/4) > sqrt(15)/sqrt(10) > sqrt(1.5) > 1.2

S > 4.8

Bon.. éventuellement affiner les minorations ci-dessus en calculant 1.25^2 (pose et effectue)

[Ben314]

Salut,
A mon avis, vu la définition même des logarithmes, pour démontrer un truc du style :
Si alors
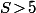
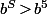
Ca me semble pas con de montrer en fait que pour un bien choisi.
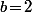
Si on prend par exemple alors on a :

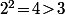
Et pour minorer les deux autres, il suffit d'écrire des trucs du style donc
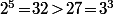
(et si ça suffit pas comme minoration, on raffine en écrivant par exemple que donc )
En procédant de la sorte, on y arrive forcément (vu qu'on a des minoration aussi précises qu'on veut) mais j'ai la flemme de regarder quelle est la valeur la plus simple pour qui donne des minorations "sympathiques".

Evidement, il y a éventuellement des solutions plus rapides....

[FLBP]

Bravo à tous,
J'avais la méthode de Lostounet, voilà ma solution détaillée :

Moyenne géométrique Moyenne arithmétique

Du coup :



Supposons que :











Supposons que :





Supposons que :







Voilà, l'inéquation est correcte

[Pseuda]

Bonsoir,

Avec l'IAG :







Sympa. (sauf erreur ?)

[MMu]

@Pseuda : ta solution ne marche pas puisque si alors et non l'inverse

[Pseuda]

En effet, grossière erreur.

C'est : ,
mais cela n'aboutit pas (on est déjà en-dessous).

[Pseuda]

Bonjour,

@FLBP, il s'agit de montrer que :

.

C'est immédiat sachant que .