salut
THE : le produit de n entiers consécutifs est multiple de n
DEM : la division euclidienne (on peut travailler avec des modulos pour aller plus vite)
donc p(p - 1)(p + 1) est évidemment multiple de 3 et de 2 (qui sont premiers entre eux donc de 6)
REM : un multiple de 3 et de 6 n'est pas toujours multiple de 18 :: EX : 12 !!!)
mais oublions ce facteur 2 pour l'instant ...
et il reste donc à montrer que
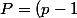^2p(p + 1))
est multiple de 16
p est impair donc p - 1 et p + 1 sont pairs et l'un est multiple de 4 puisqu'un pair sur deux est multiple de 4
il est donc évident que quelle que soit la situation
^2(p + 1))
est multiple de 16 puisqu'on a les situations
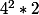
et
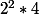
qui sont tous deux multiples de 16
(c'est même multiple de 32 une fois sur 2)

Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)
![Dan.San :]](https://www.maths-forum.com/images/smilies/8.gif)