Factorisation de 6 termes

[jygl]

Bonsoir !

Parmis mes exos de TD j'ai une factorisation à faire :


Je l'ai trouvée par "tâtonnement..." :

Le problème : comment justifier, ou comment trouvé sans tâtonner.

Un ami m'a expliqué qu'il a considéré comme fixé, et a factorisé un polynôme de en fonction de ses racines.

J'ai essayé, mais ça a fait beaucoup de cambouis pour pas grand chose...

L'autre méthode consistait à considérer la solution de la forme et de résoudre un système de 6 équations à 6 inconnues.
Mais encore une fois le résoudre revient à tâtonner (on "suppose , etc...")

Qu'en pensez vous ?

Merci!

[Lostounet]

Salut,
Ton ami a une idée sympa. Si on écrit l'expression:
2x^2 + (5y+3)x + (2y^2+3y+1)=0

Je considère que y est un nombre fixé. Cela te fait un trinôme du second degré de discriminant:
(5y+3)^2-8(2y^2+3y+1)
= 25y^2 + 30y + 9 - 16y^2 - 24y - 8
= 9y^2 + 6y + 1
= (3y+1)^2

qui est toujours positif!

On a donc la factorisation:
a(x-x1)(x-x2)

avec a=2
x1=(-(5y+3)-(3y+1))/2 = (-8y-4)/4=-2y-1
x2 = (-(5y+3)+(3y+1))/2 = (-2y-2)/4=(-y-1)/2

Donc (2x+y+1)(x+2y+1)

[jygl]

Hum okay !

En fait je m'étais arrêté parce que j'avais considéré le cas ou (3y+1)^2 = 0
Du coup je pensais faire 2 factorisation en fonction de y positif ou nul... (et donc une ou 2 racines)
Et ça se compliquait un peu trop à mon goût vu la simplicité de la solution que j'avais trouvée...

Mais c'est vrai que ça marche peu importe y... (enfin j'ai l'impression)

Merci !

[Lostounet]

Bonsoir !

Parmis mes exos de TD j'ai une factorisation à faire :

Une méthode consisterait à forcer le destin en forçant la symétrie de ce paraboloïde hyperbolique à apparaître.

Pose z=(x+y)/2 et t=(x-y)/2
de sorte que x=z+t et y=z-t
Comme
2(z+t)^2+2(z-t)^2 + 5(z+t)(z-t) + 6z + 1 = 0

En développant tout
(3 z + 1)^2 - t^2 = 0

(3z+1-t)(3z+1+t)=0

On repasse à x et y

(3(x+y)/2+1-(x-y)/2)(3(x+y)/2+1 +(x-y)/2)=0

Soit (x + 2y + 1)(2x+y+1)=0

[jygl]

Euh, je ne sais pas encore ce qu'est un paraboloïde hyperbolique...
Mais merci encore pour cette nouvelle méthode !

[aviateur]

Bonjour
Ok @lostounet, sauf que je ne vois pas l'équation d'un paraboloïde hyperbolique mais plutôt l'équation d'une conique.
Une conique étant une courbe du plan d'équation p(x,y)=0 où p est un polynôme de degré 2.

Ici on a p(x,y)=2x^2+2y^2+5xy+3x+3y+1
Cette factorisation montre donc que la conique p(x,y)=0 est dégénérée, c'est la réunion de 2 droites.

[Lostounet]

Oui sorry j'avais vu 'autre chose'...

z=2x^2+2y^2+5xy+3(x+y)+1

Mais en tout cas cela marche heureusement. C'est en fait l'équation d'un chips Pringles non? (si on modifie un peu les coefficients)

[aviateur]

Il faut peut être vérifier la définition exacte d'une conique, peut être qu'il faut dire de degré au plus 2.

[Lostounet]

En tout cas, il faut que je révise (aussi) les définitions exactes des paraboloides hyperboliques ou elliptiques. Je ne sais plus lequel est lequel...Je crois qu'ici via le changement de repère on est bien dans le cas 'pringle'

En l'occurrence ici oui on est dans l'intersection du chips avec z= 0 ! Et il est clair via la factorisation que l'on est sur la réunion de deux droites y=mx+p. Merci de le préciser Aviateur.

[zygomatique]

salut

l'équation générale donc cartésienne d'une droite est

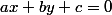
de même que le produit de deux fonctions affines et donne une fonction trinome du second degré

le produit de deux polynomes du premier degré en les variables x et y et donne une fonction polynome du second degré en les variables x et y

donc du type :

on dont donc résoudre l'équation :




je ne sais pas si l'application est surjective mais il est certain qu'elle n'est pas injective puisque :: (+)

donc si on a une solution on en a une infinité ... tout le pb est donc d'en trouver une ...


tu parles de tatonner plutôt que de mécaniquer !!!! (résoudre le système) donc de penser plutôt que d'être bourrin ben c'est bien ...

tout en sachant que l'un n'est pas exclusif de l'autre :

le tâtonnement c'est utiliser son savoir et son expérience sur le second degré car P n'est simplement qu'un polynome du second degré en x et y

la mécanique c'est travailler et calculer proprement

par exemple on voit que le terme constant de P est le produit des termes constants de p et q ...


combien de fois vous a-ton demandé une solution approchée d'une équation f(x) = 0 ou le rang à partir duquel la suite est ... ne tatonnez-vous pas ... avec ou sans machine ...

c'est une méthode de résolution


à une des dernières questions d'un exercice d'arithmétique de licence en partiel il était demandé :
pouvez-vous trouver deux entiers x et y tels où a, b, c étaient des relatifs donné ...

bien sur tous le pb consistait à résoudre cette équation ... j'avais répondu globalement à ce qui précédait (l'exo n'était pas trop dur )mais à cette question j'ai simplement répondu :

avec un petit programme ma calculatrice me dit que les entiers x = ... et y = ... sont solutions !!!

(j'avais bien sur quand même vérifié au brouillon)

mais un algorithme est une preuve (après avoir prouvé que l'algo est ""exact"" : voir théorème des quatre couleurs)

maintenant pour factoriser (comme en première) :

avec des entiers on espère évidemment une solution ""simple"" : des relatifs ... et au pire éventuellement des fractions ""élémentaires""

le système d'équation nous fait fortement penser que (en travaillant dans les entiers les conditions de divisibilité sont restreintes ... très restreintes ... puisque tout entier ne divise que ses multiples !!! ) que (*)

le développement montre que les trois premiers termes sont égaux .... reste à déterminer les réels a et b avec l'expression 3x + 3y + 1 (trois équations à deux inconnues : ha tiens le système peut éventuellement ne pas avoir de solutions auquel cas l'application ne serait pas surjective non plus)

le tâtonnement (travail intérieur basé sur des savoirs et savoir-faire) conduit à proposer (*)
la mécanique nous permet de résoudre le système (enfin très réduit : trois équation à deux inconnues mais surtout linéaire)

ce qui nous permet de justifier (+)

[Ben314]

Salut,

...je ne sais pas si l'application est surjective...

Non, surement pas : si ton polynôme P (en deux variables x,y et de degré 2) s'écrit comme produit de deux polynôme de degré 1 (en x et y), cela implique que l'ensemble des solutions de l'équation P(x,y)=0 est constitué de la réunion de deux droites or ce n'est clairement pas le cas par exemple pour P(x,y)=x²+y²-1 où l'ensemble des solutions c'est le cercle trigo.
En fait, contrairement aux polynômes en une seule variable, pour un polynôme de degré 2 en x,y c'est plutôt "exceptionnel" qu'il puisse se factoriser en deux polynômes de degré 1, même si on accepte des coefficients complexes : si on regarde les solutions de P(x,y)=0, en général, c'est une conique (réelle ou complexe) et le cas où P se factorise en deux polynômes de degré 1 correspond au cas d'une "conique dégénérée" qui est la réunion de deux droites.

Edit :
En fait se factorise ssi

[Ben314]

Sinon, concernant "ce que c'est" (paraboloïde ? conique ?), ben faudrait évidement savoir de quoi on parle.

- P lui même, c'est un polynôme donc c'est pas du tout un ensemble de point donc surement pas une conique ou un paraboloïde ou quoi que ce soit de ce genre...

- L'ensemble des solutions de l'équation P(x,y)=0, c'est une partie de R² qui, comme P est de degré 2, est une conique, sauf que dans le cas présent, c'est une conique dégénérée : c'est la réunion de deux droites.

- Le graphe de P, c'est à dire l'ensemble des (x,y,z) tels que z=P(x,y), c'est cette fois une partie de R^3 et pas de R² et c'est effectivement un paraboloïde et il est hyperbolique vu que le discriminant b²-4ac=5²-4x2x2=9 est >0


Sinon, une légère variante par rapport à la méthode proposée par Lostounet, c'est de voir que, si (*)
alors donc, c'est à dire et les outils classiques vu au Lycée permettent de trouver sans ambiguïté a,b et e.
Il reste à injecter ces valeur dans la relation de départ (*) et à voir s'il existe c et e tels que ça marche (et c'est là qu'il n'est pas du tout évident qu'il y ait des solutions vu qu'on a 3 équation et deux inconnues)

[zygomatique]

bien sur je faisais un peu le naïf dans ma réflexion ... (découverte au fur et à mesure des choses) ...

mais merci pour les compléments : en particulier pour la condition équivalente d'existence ... et qui répond à la question de surjectivité ...

effectivement c'était quasi évident avec le polynome"" élémentaire"" correspondant à l'équation du cercle :

et un peu de rappel sur le vocabulaire et définition des objets et dans quel espace on se place ne semble pas faire de mal non plus ...


merci

[aviateur]

Bonjour
Effectivement @Lostounet si tu considères la surface S d'équation z=f(x,y) cela ressemble bien à une chips.
J'ai fait 2 représentations graphiques mais malheureusement je n'arrive pas à les télécharger.
L'intersection de S avec le plan d'équation z=cste semble en général être une hyperbole.
Avec z= 0 c'est une réunion de 2 droites.
Se pose alors la question suivante: quelles sont les droites qui sont incluses dans S?
Suite à cette question, S est-elle générée par une famille de droites?

[Lostounet]

Salut Aviateur,

As-tu essayé d'héberger les captures d'écran sur un autre site?
Il semble qu'il y a un pb sur les fichiers du forum.

[aviateur]

Capture d'écran sur un autre site, c'est à dire?

[Ben314]

@Aviateur :
Oui : un paraboloïde hyperbolique est effectivement une surface réglée, c'est à dire constitué d'une réunion de droites.
En fait, il est même "doublement réglé", c'est à dire qu'en tout point M du paraboloïde hyperbolique P, il existe DEUX droites distinctes D1 et D2 contenant M et contenues dans P.
En faisant un changement de repère (non orthonormé) sur le plan de base et une translation sur l'axe des z, tout paraboloïde hyperbolique admet une équation de la forme z=x²-y² et on vérifie aisément que pour un point M:(a,b,c) fixé de P, l'intersection du paraboloïde avec le plan tangent en M à P est constitué de deux droites (dirigées respectivement par (1,1,2(a-b)) et par (1,-1,2(a+b)).

[aviateur]

Oui merci @ben314. Je m'en doutais un peu mais sans en être sûr.