Aidez moi

[jenni00122]

J'ai un petit exo ke je ne compren pa tré bien
on me demande de trouver les solutions de f(x)=0
sachant que f(x)=x^3-3x²-5x-2,01
merci d'avance

[fonfon]

salut,

c'est bien

si c'est ça pour resoudre f(x)=0 je pense qu'il faut faire une etude de fonction et utiliser le theoreme de bijection (car il n'y a pas de racine evidente)

[jenni00122]

salut,

c'est bien

si c'est ça pour resoudre f(x)=0 je pense qu'il faut faire une etude de fonction et utiliser le theoreme de bijection (car il n'y a pas de racine evidente)

oui c'est bien ça mais c'est quoi le théorème de bijection?

[fonfon]

re,

oui c'est bien ça mais c'est quoi le théorème de bijection?

1ere redaction:

Soit f une fonction continue et strictement monotione sur l'intervalle I.

Alors f est une bijection de I sur l'intervalle image J=f(I), c'est à dire que pour tout réel u de l'intevalle J a un antecedent unique x ds I tel que f(x)=u

autre redaction possible:

Si la fonction est derivable sur I, on determinie le tableau de variation.

Lorsque la fonction est monotone sur un intervalle [a,b] de I et que f(a) et f(b) sont de signes contraires, alors il existe un seul nombre réel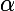 appartenant à ]a,b[ tel que

[jenni00122]

ah ok merci bcp