Limite fonction

[mehdi-128]

Bonjour,

Soit p un entier naturel, déterminer :

Je voulais partir de :

Merci

[Mimosa]

Bonjour

Tu dis qui est et tu pars comme tu en avais l'intention! Tu verras bien où tu arrives.

[mehdi-128]

p et q sont des entiers naturels quelconques ...

[mehdi-128]

La puissance q sur le logarithme me gêne

[Mimosa]

Si on a

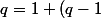[mehdi-128]

Mimosa si q=0 la limite est clairement nulle et si q>0 :



Ca m'avance à quoi ?

[FLBP]

Salut,
Normalement, en répétant q fois Bernoulli-l'Hospital tu trouves :



Cordialement.

[mehdi-128]

D'accord FLBP

Le cours de sup donne pour tout alpha et beta >0 :

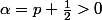
Je prends : si q est nul la limite donne 0 donc je prends beta à partir de 1 :


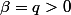
Je suis dans ce cas après je comprends pas la valeur absolue sur le ln

[zygomatique]

parce que si beta = pi par exemple alors comment calcules-tu (-3)^pi ?

[MJoe]

D'accord FLBP

Le cours de sup donne pour tout alpha et beta >0 :

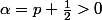
Je prends : si q est nul la limite donne 0 donc je prends beta à partir de 1 :


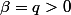
Je suis dans ce cas après je comprends pas la valeur absolue sur le ln

Bonjour medhi et bonjour à tous,

On ne peut pas élever un nombre négatif à une puissance autre qu'une puissance entière. C'est pour cela que la valeur absolue sur le "ln()" est nécessaire.
Un autre exemple sur ce sujet.

MJoe.

[mehdi-128]

D'accord FLBP

Le cours de sup donne pour tout alpha et beta >0 :

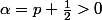
Je prends : si q est nul la limite donne 0 donc je prends beta à partir de 1 :


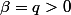
Je suis dans ce cas après je comprends pas la valeur absolue sur le ln

Bonjour medhi et bonjour à tous,

On ne peut pas élever un nombre négatif à une puissance autre qu'une puissance entière. C'est pour cela que la valeur absolue sur le "ln()" est nécessaire.
Un autre exemple sur ce sujet.

MJoe.

D'accord j'ai compris mais dans ma rédaction quand je veux calculer la limite en 0 par exemple de je met ln(t) ou -ln(t) car je sais pas si ma valeur absolue du logarithme |ln(t)| vaut + ln(t) ou -ln(t) ?

[zygomatique]

connais-tu le signe de ln x en fonction de x ?

[mehdi-128]

connais-tu le signe de ln x en fonction de x ?

Bah ln(x) < 0 pour x<1 et ln(x) >0 pour x>1

Donc quand on fait la limite en 0+ faudrait mettre - ln(x) non ?

[zygomatique]

https://www.ilemaths.net/sujet-equivale ... msg6545787 ...