Est ce que quelqu'un saurait résoudre ce problème d'optimisation ?? merci d'avance
Problème d'optimisation
2 messages
- Page 1 sur 1
problème d'optimisation
par natikozlo » 28 Aoû 2017, 11:22
Dans le plan rapporté à un repère orthonormé d’origine O et d’axes x et y, on considère le point P (2, 4). Déterminer l’équation de la droite de coefficient angulaire négatif et passant par P qui délimite avec les axes x et y une surface d’aire minimale.
Est ce que quelqu'un saurait résoudre ce problème d'optimisation ?? merci d'avance
Est ce que quelqu'un saurait résoudre ce problème d'optimisation ?? merci d'avance
Re: problème d'optimisation
par Razes » 28 Aoû 2017, 13:10
Bonjour,,
Soit l'équation de la droite (D):
(D) passe par\Rightarrow 2a+b=4\Leftrightarrow b=4-2a)
l'équation de la droite (D) devient: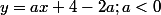
(D) rencontre l'axe des)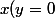
en )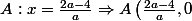
(D) rencontre l'axe des)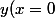
en )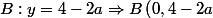
La surface du triangle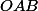
: =\frac{1}{2}OA\times OB=\frac{1}{2}\left ( \frac{2a-4}{a} \right )\left ( 4-2a \right ))
Donc:=-\frac{1}{2} \frac{\left (2a-4 \right )^2}{a} =-2\frac{\left (a-2 \right )^2}{a})
Il faut étudier cette fonction avec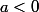
=-2\frac{(a-2)(a+2)}{a^{2}})
; donc: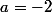 
=16)
Soit l'équation de la droite (D):
(D) passe par
l'équation de la droite (D) devient:
(D) rencontre l'axe des
(D) rencontre l'axe des
La surface du triangle
Donc:
Il faut étudier cette fonction avec
2 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 34 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :