Soit n un entier tel que :
Soit x fixé :
J'aimerais déterminer la limite de fn pour : x<0 et x>0 .
Pour x<0 j'aimerais montrer que fn ne tend pas vers 0.
En x=0 ça tend vers 0.
* Pour x<0 :
Le
Limite de suite
10 messages
- Page 1 sur 1
Limite de suite
par mehdi-128 » 17 Aoû 2017, 15:16
Bonjour,
Soit n un entier tel que :
Soit x fixé : = \frac{(-1)^{n-1}}{n^x})
J'aimerais déterminer la limite de fn pour : x<0 et x>0 .
Pour x<0 j'aimerais montrer que fn ne tend pas vers 0.
En x=0 ça tend vers 0.
* Pour x<0 : = (-1)^{n-1} exp(-x \times ln(n)))
Le^{n-1})
me gêne ...
Soit n un entier tel que :
Soit x fixé :
J'aimerais déterminer la limite de fn pour : x<0 et x>0 .
Pour x<0 j'aimerais montrer que fn ne tend pas vers 0.
En x=0 ça tend vers 0.
* Pour x<0 :
Le
Re: Limite de suite
par NicoTial » 17 Aoû 2017, 15:35
Bonjour,
Pour x>0, tu peux y arriver facilement avec le critère spéciale des séries alternées par exemple.
Pour x>0, tu peux y arriver facilement avec le critère spéciale des séries alternées par exemple.
Re: Limite de suite
par NicoTial » 17 Aoû 2017, 15:40
Et pour x<0, ta suite de fonction ne tend pas du tout vers 0 !
Re: Limite de suite
par zygomatique » 17 Aoû 2017, 17:02
salut
si x < 0 alors = (-1)^{n - 1} n^{|x|})
...
si x < 0 alors
Ce qui est affirmé sans preuve peut être nié sans preuve. EUCLIDE
Re: Limite de suite
par mehdi-128 » 17 Aoû 2017, 18:05
zygomatique a écrit:salut
si x < 0 alors
Donc :
La limite de l'exponentielle tend vers + l'infini mais comment faire avec le (-1)^(n-1) ?
Re: Limite de suite
par mehdi-128 » 17 Aoû 2017, 18:08
NicoTial a écrit:En x=0, es-tu sûr de ce que tu avances ?
En effet je me suis trompé :
Quelle est la limite de fn(0) ?
Si je montre qu'elle est différente de 0 alors ma série sera grossièrement divergente
Re: Limite de suite
par mehdi-128 » 17 Aoû 2017, 20:26
Je dirai qu'en 0, la suite de fonction n'a pas de limite (oscille entre 1 et -1) et donc la série diverge grossièrement.
Pour x<0 : Pareil la suite de fonction n'a pas de limite ça oscille entre + l'infini et - l'infini donc la série diverge grossièrement.
Pour x>0 :|=\frac{1}{n^x})
ce qui tend vers 0 en + l'infini.
Il faut montrer que|)
est décroissante.
Je fais :|}{|f_n(x)|}=(\frac{n}{n+1} )^x)
On a :
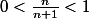
La fonction u --> u^x (x positif) est elle croissante sur ]0,1[ ?
Pour x<0 : Pareil la suite de fonction n'a pas de limite ça oscille entre + l'infini et - l'infini donc la série diverge grossièrement.
Pour x>0 :
Il faut montrer que
Je fais :
On a :
La fonction u --> u^x (x positif) est elle croissante sur ]0,1[ ?
Re: Limite de suite
par mehdi-128 » 17 Aoû 2017, 22:15
J'ai fait : pour x>0 :
}{f_n (x)}| =exp (|x| \times ln(\frac{n}{n+1})))
Or :
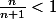
donc  <0)
Donc}{f_n (x)}| < 1)
Donc (|fn(x)|) est décroissante
Or :
Donc
Donc (|fn(x)|) est décroissante
Re: Limite de suite
par NicoTial » 18 Aoû 2017, 09:25
mehdi-128 a écrit:
La fonction u --> u^x (x positif) est elle croissante sur ]0,1[ ?
Tu peux répondre à cette question tout seul avec une simple étude de fonction.
Bon à partir de là, tu peux conclure immédiatement.
10 messages
- Page 1 sur 1
Qui est en ligne
Utilisateurs parcourant ce forum : Aucun utilisateur enregistré et 32 invités
Tu pars déja ?
Fais toi aider gratuitement sur Maths-forum !
Créé un compte en 1 minute et pose ta question dans le forum ;-)
Identification
Pas encore inscrit ?
Ou identifiez-vous :