Lieu géométrique.

[HaiatAsmaa]

Bonjour,
Je bloque sur l'exercice suivant, quelqu'un a une idée svp? Merci.

Dans le plan euclidien rapporté au système d’axes orthonormés Oxy, on considère un point
variable P sur le cercle de centre C(2, 0) et de rayon unité.

Déterminez la nature et une équation
cartésienne du lieu parcouru par le point Q si le triangle OPQ est isocèle et rectangle en O

[cailloux1]

Bonjour,

Géométriquement, les rotations de centre et d' angle 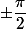ont leur mot à dire

[MJoe]

Bonjour à tous,

L'affixe du point P est :
On a :
Lieu N°1 :
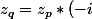ce qui donne :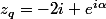
ou :
Lieu N°2
ce qui donne :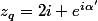

Le lieu N°1 est le cercle de centre B(0;-2) et de rayon 1. Son équation cartésienne est :
Le lieu N°2 est le cercle de centre C(0;2) et de rayon 1. Son équation cartésienne est :

Un dessin sur Geogebra :



MJoe.

[HaiatAsmaa]

Merci MJoe,
Mais pour mon niveau, je n'ai pas encore vu les complexes en Géométrie, je cherchais une solution on utilisant la rotation et les coordonnées des points P et Q. C'est un examen pour la polytech

[cailloux1]

Sans passer par les complexes, le point est l' image du point dans la rotation de centre et d' angle 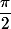(respectivement 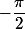) suivant que le triangle 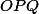est rectangle isocèle en direct (respectivement indirect).

Le lieu de est donc l' image du lieu de dans ces deux rotations à savoir les deux cercles de centre et de rayon respectivement de centre et de rayon

Il est facile de déterminer une équation cartésienne de ces deux cercles.

[HaiatAsmaa]

Un tous grand merci cailloux1.

[Razes]

Déterminez la nature et une équation cartésienne du lieu parcouru par le point Q si le triangle OPQ est isocèle et rectangle en O

Bonjour,

cercle de centre (1)

Soit A déterminer

Le triangle est isocèle et rectangle en , Donc: , d'où (2)

(3)

Reste à extraire en utilisant (1), (2) et (3)

[Razes]

car sinon et l'équation serait impossible.

Donc devient:

De plus
Donc il faut discuter le cas .

Cas:


Cas:


Si ; les solutions seront: et
Si ; les solutions seront: et